자전거 대여 수요 예측을 위한 머신러닝 모델 구축

Posted Nov 30, 2024

By Sun Hyuk Kim

23 min read

1. 분석 배경 및 목적

분석 배경 : 워싱턴 D.C.의 A사 자전거 대여 시스템 운영 담당자로서 자전거 대여 패턴을 분석하여 자전거 배치와 운영 전략을 최적화하고, 대여 수요를 정확히 예측하고자 한다
분석 목적 : 자전거 대여 시스템의 효율성을 높이고 사용자 만족도 증가
분석 목표 : 머신러닝 모델을 실험하여 RMSLE를 낮추는 최적의 자전거 대여 수요 예측 모델 개발
- RMSLE란? : Root Mean Squared Logarithmic Error의 약자로, 예측 값과 실제 값의 차이를 로그 변환하여 계산한 후, 그 차이의 제곱 평균의 제곱근을 구한 값이다
  - 이 지표는 예측 오차를 측정하는데 사용되며, 특히 큰 값보다 작은 값의 오차를 더 중요시하는 지표이다
  - 예측 값이 실제 값보다 훨씬 클 때 더 큰 패널티를 부과하므로, 예측 값이 과대평가되는 것을 방지하는데 효과적이다
  - 예측 값과 실제 값이 0에 가까울 경우에도 로그 변환을 통해 안정적인 값을 산출한다
  - 예측 값이 실제 값보다 훨씬 클 때 더 많은 패널티를 부과하여 과대평가를 방지하고 모델의 신뢰성을 높인다

\[RMSLE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\log(y_i + 1) - \log(\hat{y}_i + 1))^2}\]

2. 데이터 소개

본 데이터셋은 워싱턴 D.C.의 A사 자전거 대여 시스템의 데이터이며 날씨, 계절, 시간 등의 데이터가 포함되어 있다
기간 : 2011년 ~ 2012년 자전거 대여 데이터

컬럼명	데이터 타입	설명
datetime	datetime	자전거 대여 기록의 날짜 및 시간. 예시: 2011-01-01 00:00:00
season	int	계절 (1: 봄, 2: 여름, 3: 가을, 4: 겨울)
holiday	int	공휴일 여부 (0: 평일, 1: 공휴일)
workingday	int	근무일 여부 (0: 주말/공휴일, 1: 근무일)
weather	int	날씨 상황 (1: 맑음, 2: 구름낌/안개, 3: 약간의 비/눈, 4: 폭우/폭설)
temp	float	실측 온도 (섭씨)
atemp	float	체감 온도 (섭씨)
humidity	int	습도 (%)
windspeed	float	풍속 (m/s)
casual	int	등록되지 않은 사용자의 대여 수
registered	int	등록된 사용자의 대여 수
count	int	총 대여 수 (종속 변수)

3. EDA

3-1. 기초 데이터 파악

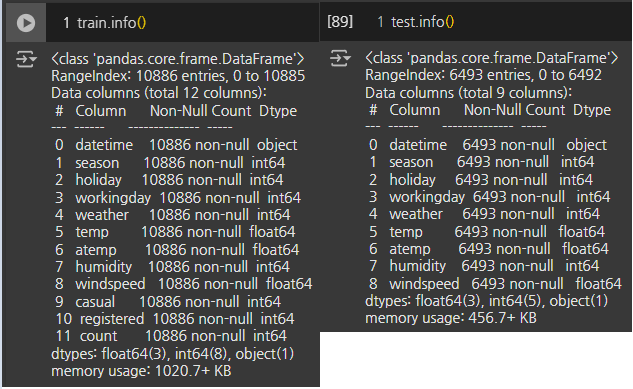
훈련데이터(train) : 10,886행 12열 데이터로 구성되어있다
- datetime열부터 registered열까지 자전거 대여 수count를 예측하는데 사용되는 컬럼이며, count는 casual(비회원)과 registered(회원)의 자전거 대여 수 합계를 나타낸다
- 다만, test데이터에 casual, registered열이 없기때문에 모델 훈련시 해당 컬럼을 제외해야한다
테스트데이터(test) : 6,493행 9열 데이터로 구성되어있다
- 훈련데이터(train)의 casual과 registered, count열이 포함되어있지 않았다
데이터 타입 : 2. 데이터 소개컬럼 표에 나와있듯이 데이터 타입은 훈련 데이터와 테스트 데이터가 동일하였다

3-2. 데이터 전처리

3-2-1. 결측치 처리

훈련 데이터와 테스트 데이터 모두 결측값이 관찰되지 않았다

3-2-2. 파생변수 생성

현재 데이터 상 datetime열은 object타입으로 연도, 월, 일, 시간, 분, 초로 구성되어있다
- 예시 : 2011-01-01 10:00:00
원활한 분석을 위해 datetime이 문자열로 묶여있는부분을 각각 풀어서 파생변수를 생성하여 활용하고자 한다
datetime열을 각각 세분화하고 요일 파생변수도 추가하였다

  
train['date'] = train['datetime'].apply(lambda x: x.split()[0]) # 날짜 변수 생성

# 연도, 월, 일, 시, 분, 초 변수를 차례로 생성
train['year'] = train['datetime'].apply(lambda x: x.split()[0].split('-')[0])
train['month'] = train['datetime'].apply(lambda x: x.split()[0].split('-')[1])
train['day'] = train['datetime'].apply(lambda x: x.split()[0].split('-')[2])
train['hour'] = train['datetime'].apply(lambda x: x.split()[1].split(':')[0])
train['minute'] = train['datetime'].apply(lambda x: x.split()[1].split(':')[1])
train['second'] = train['datetime'].apply(lambda x: x.split()[1].split(':')[2])

# 요일 변수 생성
train['weekday'] = train['date'].apply(
    lambda dateString:
    calendar.day_name[datetime.strptime(dateString, "%Y-%m-%d").weekday()])

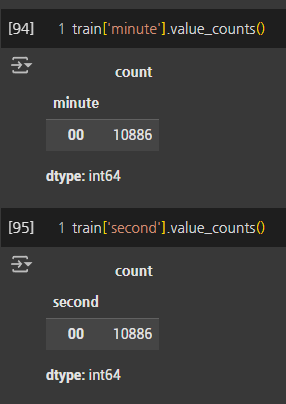
자전거 대여 정보는 1시간 단위로 기록되는 것으로 파악되어 분, 초 단위는 삭제하였다

  
train = train.drop(['minute', 'second'], axis=1)

3-2-3. 데이터 매핑

원활한 시각화 분석을 위해 season, weather열을 숫자에서 문자열로 변환하였다

  
train['season'] = train['season'].map({1: 'Spring',
                                       2: 'Summer',
                                       3: 'Fall',
                                       4: 'Winter'})

train['weather'] = train['weather'].map({1: 'Clear',
                                         2: 'Mist, Few clouds',
                                         3: 'Light Snow, Rain',
                                         4: 'Heavy Snow, Rain'})

3-3. 데이터 시각화

3-3-1. datetime 시각화

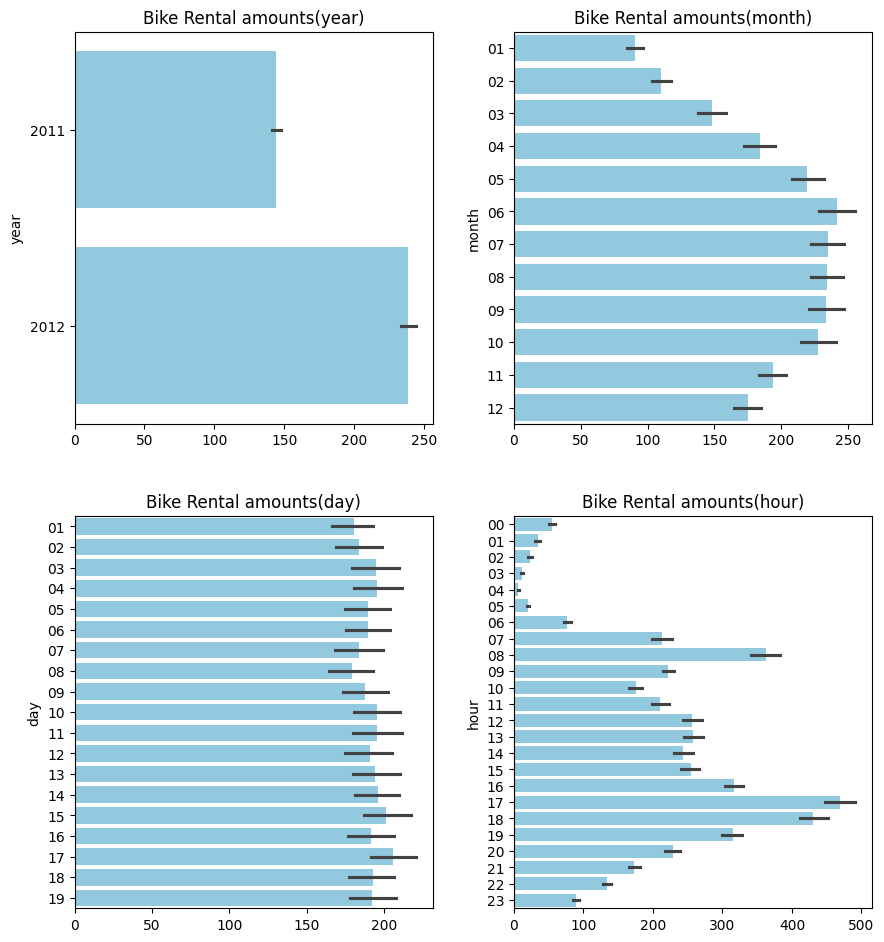
datetime열을 파생변수로 세분화하여 년, 월, 일, 시간별 평균 대여 수량을 파악하였다

연도별 평균 대여 수량은 2011년보다 2012년에 더 많은것으로 관찰되었다
월별 평균 대여 수량은 6월에 가장 많고 1월에 가장 적은것으로 관찰되며, 날씨가 추운날보다 따뜻한날에 대여수량이 많은것으로 관찰되었다
일별 평균 대여 수량은 균일해보이며, train 데이터(1일-19일)와 test 데이터(20일-31일)의 일자 기준이 달라 모델 훈련에 사용할 수 없을것으로 판단된다
시간별 평균 대여 수량은 오전 8시와 오후 5~6시에서 대여수량이 많은것으로 관찰되며, 출퇴근이나 등하교 시간대에 자전거 대여를 주로 이용하는 것으로 파악할 수 있다

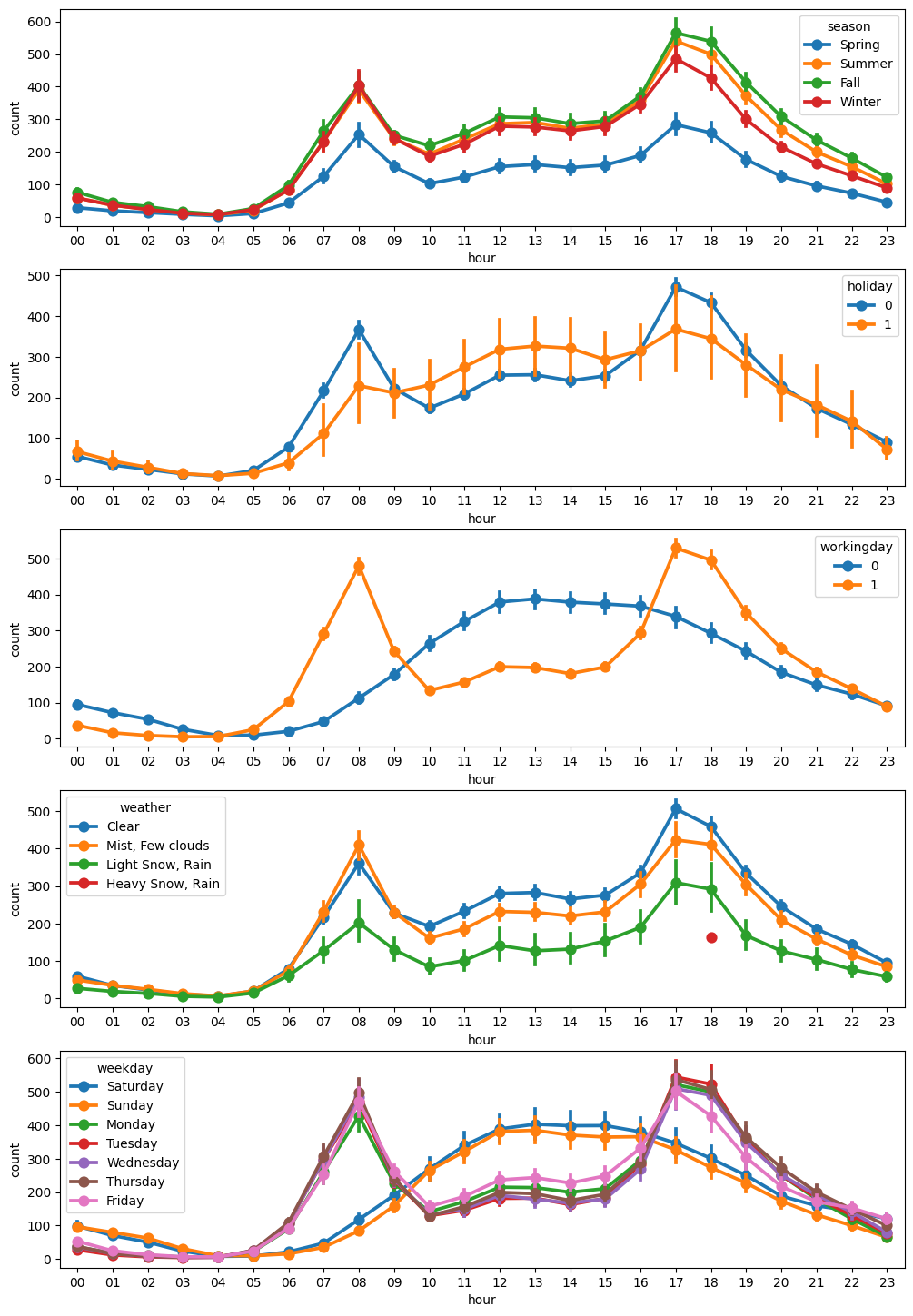
3-3-2. 계절, 공휴일, 근무일, 날씨 상황 시각화

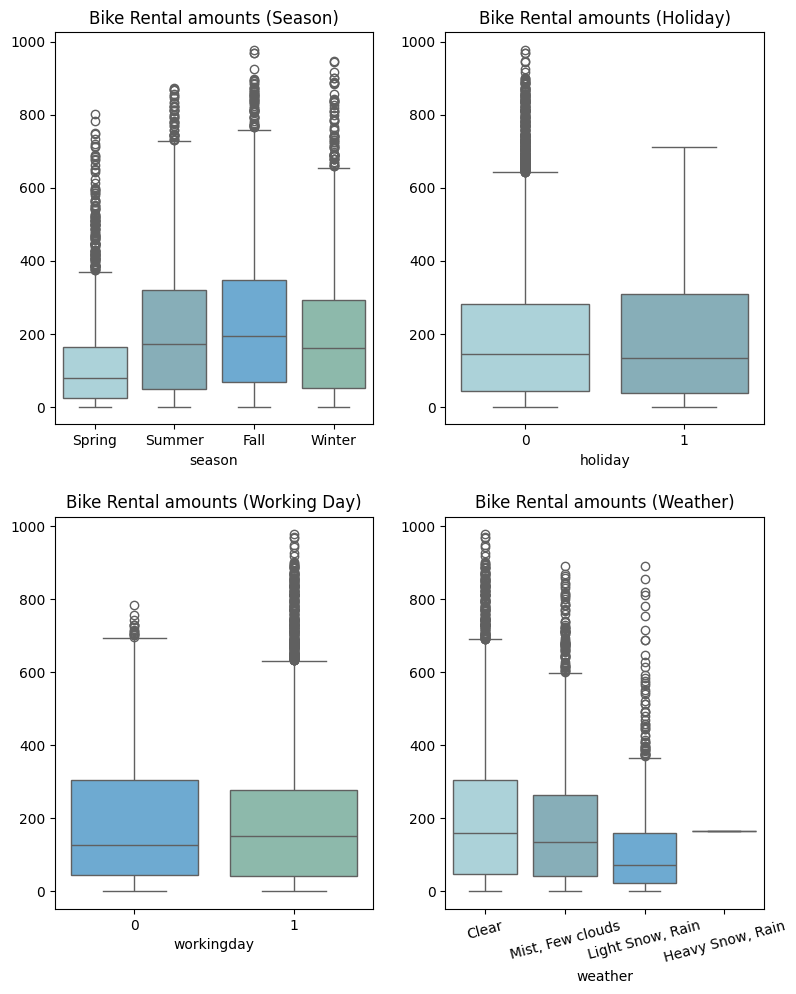
계절별 자전거 대여 수량은 봄에 가장 적고, 가을에 가장 많게 관찰되었다
공휴일 여부에 따른 자전거 대여 수량은 비슷하게 관찰됐지만 공휴일이 아닌 경우 이상치가 다수 관찰됐으며, 이는 출퇴근 일상중에 자전거를 이용하는 요인이 더 많은것으로 판단된다
근무일 여부에 따른 자전거 대여 수량도 공휴일 여부와 비슷하게 차이가 없는것으로 관찰됐으며 근무일일때 이상치가 다수 관찰되었다
날씨 상황에 따른 자전거 대여 수량은 날씨가 좋을수록 대여 수량이 많은것으로 관찰됐으며, 폭우 혹은 폭설일때 자전거 대여 수량은 거의 관찰되지않았다

근무일 혹은 평일에는 출퇴근 시간대(8시, 17-18시)에 자전거 대여 수량이 많고, 휴일에는 12-14시에 가장 많이 대여하는 것으로 관찰되었다
계절에 따른 시간대별 자전거 대여 수량도 앞서 살펴본 계절별 혹은 시간대별 자전거 대여 수량과 동일하며, 봄에 대여 수량이 상대적으로 적게 관찰되었다
날씨 상황에 따른 시간대별 자전거 대여 수량도 앞서 살펴본것처럼 날씨가 좋을수록 대여량이 많아지는 것으로 관찰되었다
- 다만, 폭우나 폭설일 때 자전거 대여는 18시에서만 1건만 관찰되고 있어 해당 데이터가 정상적인 데이터가 아닐수 있으며 이상치 제거를 고려해 볼 수 있다

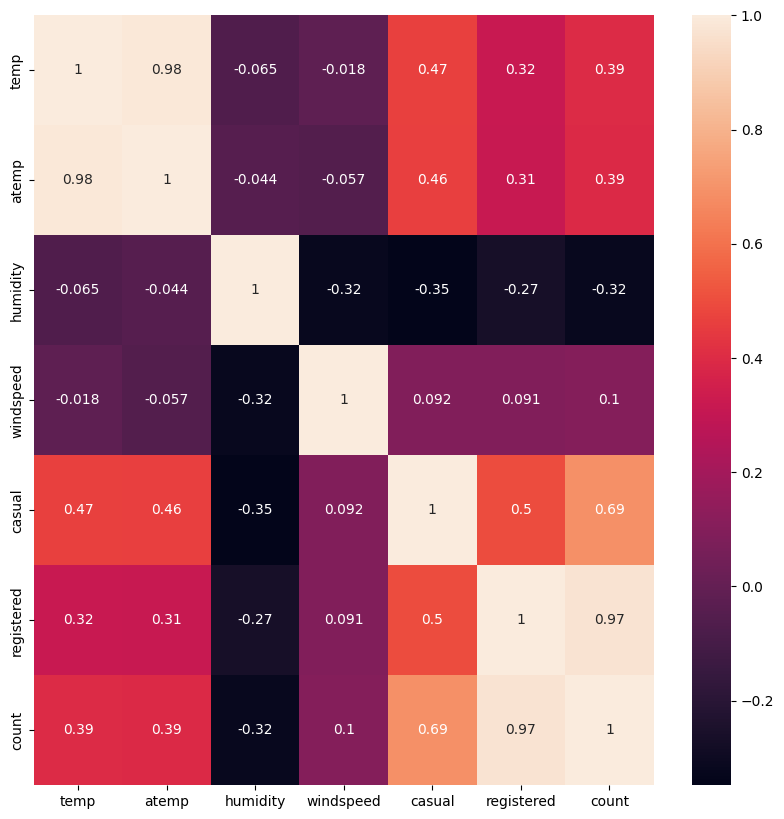
3-3-3. 상관관계 분석(온도, 습도, 풍속, 회원 여부)

히트맵 시각화

casual(비회원)과 registered(회원)는 둘의 합인 count(총 대여 수)열과 각각 강한 양의 상관관계를 보였다
온도(temp, atemp)와 대여 수량(count)간 상관계수는 0.39로 양의 상관관계를 보였으며, 이는 온도가 높을수록 대여 수량이 많아질 수 있음을 파악할 수 있다
습도(humidity)와 대여 수량(count)간 상관계수는 -0.32로 음의 상관관계를 보였으며, 이는 습도가 낮을수록 대여 수량이 많아질 수 있음을 파악할 수 있다
풍속(windspeed)과 대여 수량(count)간 상관계수는 0.1로 매우 약한 양의 상관관계를 보였으며, 이는 풍속이 자전거 대여와 상관성이 없다고 볼 수도 있다
- 다만, 일반적으로 풍속이 강하면 자전거 대여가 적을 것으로 예측되기때문에 추가적인 확인이 필요하다
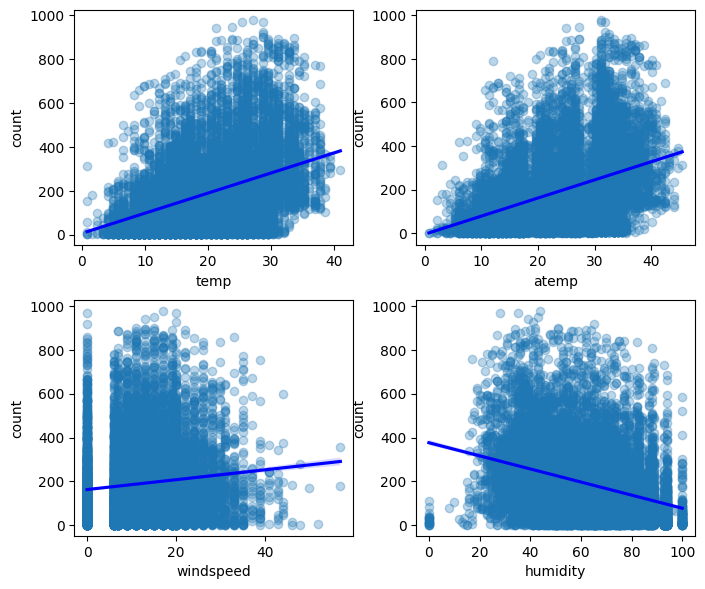
산점도 시각화

실측 온도(temp)와 체감 온도(atemp)가 높을수록 자전거 대여 수량이 많아지는 것으로 관찰되었다
습도(humidity)가 낮을수록 자전거 대여 수량이 많아지는 것으로 관찰되었다
풍속(windspeed)은 강할수록 자전거 대여 수량이 많아지는 것으로 관찰되어 일반적인 상황이라고 판단하기 어려움이 있다.
- 풍속 그래프를 확인해보니, 풍속이 0인 데이터가 상당수 있는것으로 파악되어 관측오류 혹은 집계되지 않은 풍속을 0으로 표기할 수도 있다고 판단된다.
- 이에대한 영향으로 풍속은 자전거 대여 수량(count)와 상관관계도 매우 약하게 관찰(0.1)되었기에 풍속이 0인 데이터를 다른 값으로 대체하거나 모델 학습에 고려하지 않는 방향을 검토해볼 수 있다

4. 베이스라인 모델 구축

자전거 대여 수량 예측을 위해 베이스라인 모델 구축 후 모델링 개선을 진행하고자 한다
베이스라인 모델은 앞서 진행한 EDA를 통해 모델 구축에 필요한 전처리 작업을 수행하고 진행하고자 한다

4-1. 데이터 전처리

4-1-1. 이상치 제거

데이터셋에 결측치는 발견되지 않았으나, train 데이터에서 날씨상황(weather)이 폭우 혹은 폭설인 데이터는 18시에 1건 관찰되어 이상치로 판단하여 제거하였다

  
# 폭우/폭설 데이터 제거
train = train[train['weather'] != 4]

4-1-2. train, test 데이터 결합

훈련 데이터와 테스트 데이터에 동일한 조건의 전처리를 진행하기위해 데이터를 결합하였다
다만, 본 프로젝트에서는 테스트 데이터를 사용하여 별도 제출을 하지 않았기에 테스트 데이터를 활용하지 않았다

  
all_df = pd.concat([train, test], ignore_index=True)
all_df

4-1-3. 파생변수 생성

앞서 EDA에서 생성한 datetime열 세분화 중에 train과 test의 일자가 다른점과 시간단위부터 자전거 대여 수량이 집계되는 점에서 일자, 분, 초 데이터는 파생변수로 생성하지 않았다
또한, 월(month)도 계절(season)과 차이가 없다고 판단하여 생성하지 않았다

  
# 파생 변수 생성(년, 시간, 요일)
all_df['date'] = all_df['datetime'].apply(lambda x: x.split()[0])
all_df['year'] = all_df['datetime'].apply(lambda x: x.split()[0].split('-')[0])
all_df['hour'] = all_df['datetime'].apply(lambda x: x.split()[1].split(':')[0])
all_df['weekday'] = all_df['date'].apply(lambda dateString :
datetime.strptime(dateString, "%Y-%m-%d").weekday())

4-1-4. 모델에 사용되지 않는 변수 제거

casual, registered 변수는 test 데이터에 없으므로 제거하였다
datetime, date 변수도 이미 파생변수로 생성했기에 제거하였다
풍속(windspeed) 변수도 대여 수량(count)과 상관관계가 매우 약하고 풍속이 0인 데이터가 오류 혹은 미집계로 판단되기에 제거하였다

  
all_df = all_df.drop(['casual', 'registered', 'datetime', 'date', 'windspeed'], axis = 1)

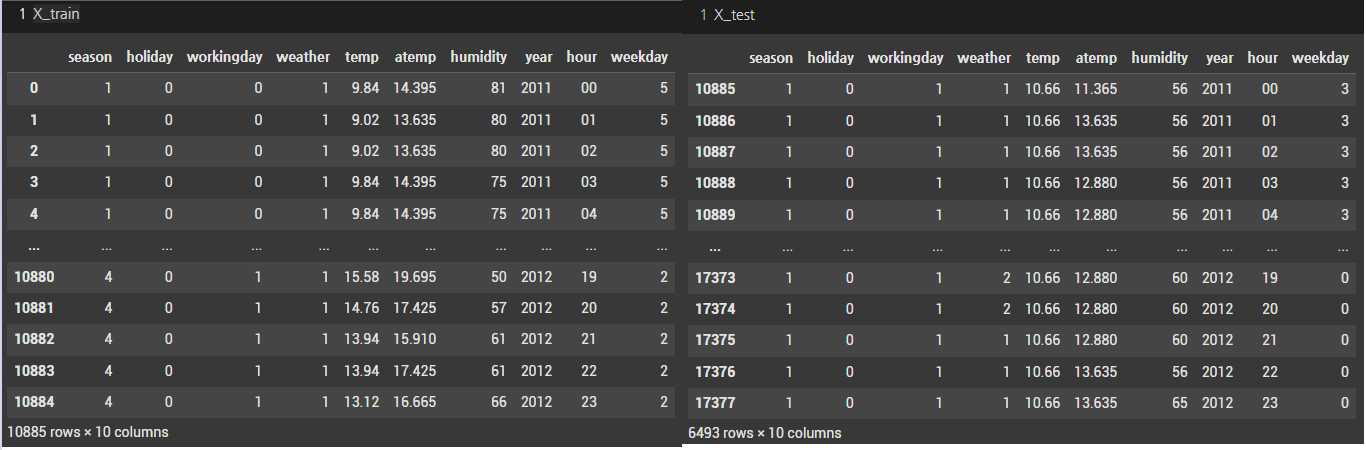
4-1-5. 데이터 분류(훈련vs테스트)

전처리 된 데이터를 train 데이터와 test 데이터로 분류하였다
- 데이터 분류는 target(count) 유무에 따라 train, test 데이터로 분류하였다
훈련 데이터에 존재했던 자전거 대여 수량을 나타내는 count데이터는 종속변수 y로 설정하였다

  
# target 유무에 따른 훈련, 테스트 데이터 분류
X_train = all_df[~pd.isnull(all_df['count'])]
X_test = all_df[pd.isnull(all_df['count'])]

# count 열 제거
X_train = X_train.drop(['count'], axis = 1)
X_test = X_test.drop(['count'], axis = 1)

# 종속변수 count 설정
y = train['count']

훈련 데이터와 테스트 데이터의 열이 일치하는 것을 확인하였다

4-2. 평가지표(RMSLE) 함수 생성

본 프로젝트 분석 목표인 RMSLE 지표를 함수로 정의하였다

  
# rmsle 함수 정의
def rmsle(y, y_, convertExp=True):
    if convertExp:
        y = np.exp(y),
        y_ = np.exp(y_)
    log1 = np.nan_to_num(np.array([np.log(v + 1) for v in y]))
    log2 = np.nan_to_num(np.array([np.log(v + 1) for v in y_]))
    calc = (log1 - log2) ** 2
    return np.sqrt(np.mean(calc))

4-3. 모델 훈련

베이스라인 모델은 선형 회귀 모델(LinearRegression)을 사용하였다

  
linear_reg_model = LinearRegression() # 모델 생성

log_y = np.log(y) # 타깃값 로그변환
linear_reg_model.fit(X_train, log_y) # 모델 훈련

preds = linear_reg_model.predict(X_train) # 모델 예측

print(f'선형 회귀의 RMSLE 값 : {rmsle(log_y, preds, True)}') # RMSLE 값 확인

모델 실험 결과 : 선형 회귀 모델의 RMSLE 값은 1.020498로 관찰되었다

5. 모델 개선

베이스라인 모델로 선택된 선형 회귀 모델보다 성능이 더 좋은 모델을 찾기위해 다양한 모델을 적용하여 비교하고자 한다

5-1. 하이퍼파라미터 튜닝(GridSearchCV)

원활한 분석을 위해 본 분석에서는 GridSearchCV를 사용하여 최적의 하이퍼파라미터 값을 찾아 모델의 성능을 비교하고자 한다
- GridSearchCV는 하이퍼파라미터를 적용한 모델마다 교차 검증(cross-validation)하며 성능을 측정하여 성능이 가장 좋은 하이퍼파라미터 값을 찾아주는 기법이다
- GridSearchCV를 사용하여 하이퍼파라미터와 값의 범위를 전달하면 최적의 하이퍼파라미터를 수작업으로 진행하지 않고 자동으로 찾기때문에 효율적으로 분석을 수행할 수 있다

5-2. 각 모델 훈련 결과 비교

모델명	RMSLE
선형 회귀 (LinearRegression)	1.0205
릿지 회귀 (Ridge)	1.0205
라쏘 회귀 (Lasso)	1.0205
랜덤 포레스트 회귀 (RandomForestRegressor)	0.1124
그레이디언트 부스팅 (GradientBoostingRegressor)	0.2278

모델 훈련 결과, 선형 회귀와 릿지, 라쏘 모델은 비슷한 성능이 관찰되었다
랜덤 포레스트 회귀 모델은 RMSLE 값이 0.11로 다른 모델에 비해 가장 큰 폭으로 개선되었다
그레이디언트 부스팅 모델은 랜덤 포레스트 회귀 모델보다 성능은 낮지만, 다른 모델보다 개선된 성능이 관찰되었다

6. 결론

본 프로젝트는 최적의 자전거 대여 수요 예측을 위해 머신러닝 모델을 실험하였다
실험결과, 랜덤 포레스트 회귀 모델이 RMSLE 값이 0.11로 자전거 대여 수요 예측 성능이 가장 높은것으로 관찰되었다
해당 모델을 통해 정확한 자전거 대여 수요를 예측하여 워싱턴 D.C.에서의 자전거 배치와 운영 전략을 최적화하는데 활용할 수 있을것이다
- 최적의 인력을 투입하여 자전거를 재배치해 운영비용을 낮추고 회전률을 높일 수 있다
- 해당 분석 결과를 활용하기위해 자전거 대여 장소별 수요를 확인할 필요가 있다
- 휴일 12-14시와 평일 출퇴근 시간대(8시, 17-18시)에 수요가 많아 자전거 대여 변화를 집중관리할 필요가 있다
- 회원과 비회원의 자전거 대여는 모두 높게 관찰되었으나, 회원 시스템의 이점(가입혜택, 가입절차 간소화 등)이 있는지 파악할 필요가 있다
- 풍속(windspeed) 정보가 명확하지 않은것으로 파악되어 데이터를 업데이트 한다면 좀 더 정확한 수요 예측이 가능할 것으로 판단된다
- 정확한 수요 예측을 위해 적합한 모델을 선정하는 과정에서 다양한 모델을 적용하는 시도를 할 필요가 있다

Data_analysis, Python_DA_Library

This post is licensed under CC BY 4.0 by the author.

1. 분석 배경 및 목적

2. 데이터 소개

3. EDA

3-1. 기초 데이터 파악

3-2. 데이터 전처리

3-2-1. 결측치 처리

3-2-2. 파생변수 생성

3-2-3. 데이터 매핑

3-3. 데이터 시각화

3-3-1. datetime 시각화

3-3-2. 계절, 공휴일, 근무일, 날씨 상황 시각화

3-3-3. 상관관계 분석(온도, 습도, 풍속, 회원 여부)

4. 베이스라인 모델 구축

4-1. 데이터 전처리

4-1-1. 이상치 제거

4-1-2. train, test 데이터 결합

4-1-3. 파생변수 생성

4-1-4. 모델에 사용되지 않는 변수 제거

4-1-5. 데이터 분류(훈련vs테스트)

4-2. 평가지표(RMSLE) 함수 생성

4-3. 모델 훈련

5. 모델 개선

5-1. 하이퍼파라미터 튜닝(GridSearchCV)

5-2. 각 모델 훈련 결과 비교

6. 결론

Trending Tags