파이썬 데이터분석 클러스터와 차원축소2

Posted Sep 22, 2024

By Sun Hyuk Kim

30 min read

  
import pandas as pd
from sklearn.cluster import KMeans
import seaborn as sns

  
pd.options.display.float_format = '{:,.2f}'.format
sales_df = pd.read_csv('/content/drive/MyDrive/sales_data.csv', index_col=['customer_id'])
sns.set(style='darkgrid',
        rc={'figure.figsize':(16,9)})
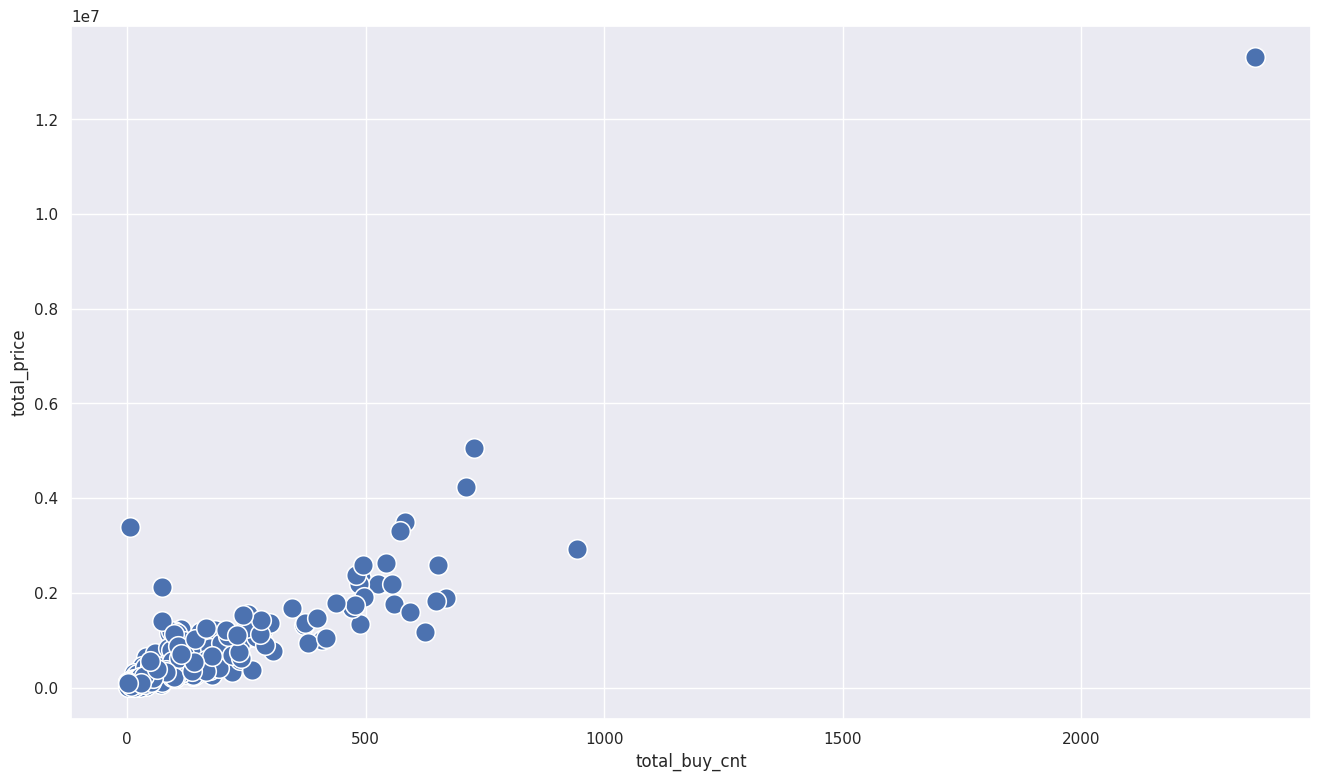
sns.scatterplot(x=sales_df['total_buy_cnt'], y=sales_df['total_price'], s=200)

<Axes: xlabel='total_buy_cnt', ylabel='total_price'>

  
# 이상치 제거
def get_outlier_mask(df, weight=1.5):
    Q1 = df.quantile(0.25)
    Q3 = df.quantile(0.75)

    IQR = Q3 - Q1
    IQR_weight = IQR * weight
    range_min = Q1 - IQR_weight
    range_max = Q3 + IQR_weight

    outlier_per_column = (df < range_min) | (df > range_max)
    is_outlier = outlier_per_column.any(axis=1)

    return is_outlier

outlier_idx_cust_df = get_outlier_mask(sales_df, weight=1.5)

sales_df = sales_df[~outlier_idx_cust_df]

# 표준화 : 평균이 0, 분산을 1로 값 조정
df_mean = sales_df.mean()
df_std = sales_df.std()

scaled_df = (sales_df - df_mean)/df_std
scaled_df.columns = ['total_buy_cnt', 'total_price']
scaled_df.index = sales_df.index

scaled_df

	total_buy_cnt	total_price
customer_id
12395	-0.05	-0.15
12427	-0.07	0.21
12431	0.23	0.95
12471	-1.13	-1.02
12472	-0.19	0.21
...	...	...
18144	-0.89	-1.04
18168	1.69	2.74
18225	-1.24	-1.04
18229	-0.67	0.19
18239	1.53	1.64

225 rows × 2 columns

모델과 학습

모델 : 분석 방법론을 의미하며, 분석법을 적용한 결과물을 저장할 수 있는 프로그램
학습 : 모델에게 데이터를 전달해서 분석을 시키는 과정
K-means 모델 학습 : k-means분석법이 저장된 프로그램에게 분석하길 원하는 데이터를 전달해서 결과물을 저장
- scikit-learn 라이브러리 사용

  
from sklearn.cluster import KMeans

  
# kmeans 함수 모델 선언
model = KMeans(n_clusters=2, random_state=21)
# n_cluster : 클러스터를 몇 개로 나누는지, k를 몇으로 설정할지 결정
# random_state : 여러번 반복해서 모델을 학습시킬 때, 동일한 결과가 나올 수 있도록 해주는 난수

# 모델 학습 : sklearn함수 fit()사용
model.fit(scaled_df)

# 클러스터 시각화
# predict() : 각 데이터가 어떤 클러스터로 구분됐는지 표시
scaled_df['label'] = model.predict(scaled_df)
scaled_df

	total_buy_cnt	total_price	label
customer_id
12395	-0.05	-0.15	0
12427	-0.07	0.21	0
12431	0.23	0.95	1
12471	-1.13	-1.02	0
12472	-0.19	0.21	0
...	...	...	...
18144	-0.89	-1.04	0
18168	1.69	2.74	1
18225	-1.24	-1.04	0
18229	-0.67	0.19	0
18239	1.53	1.64	1

225 rows × 3 columns

  
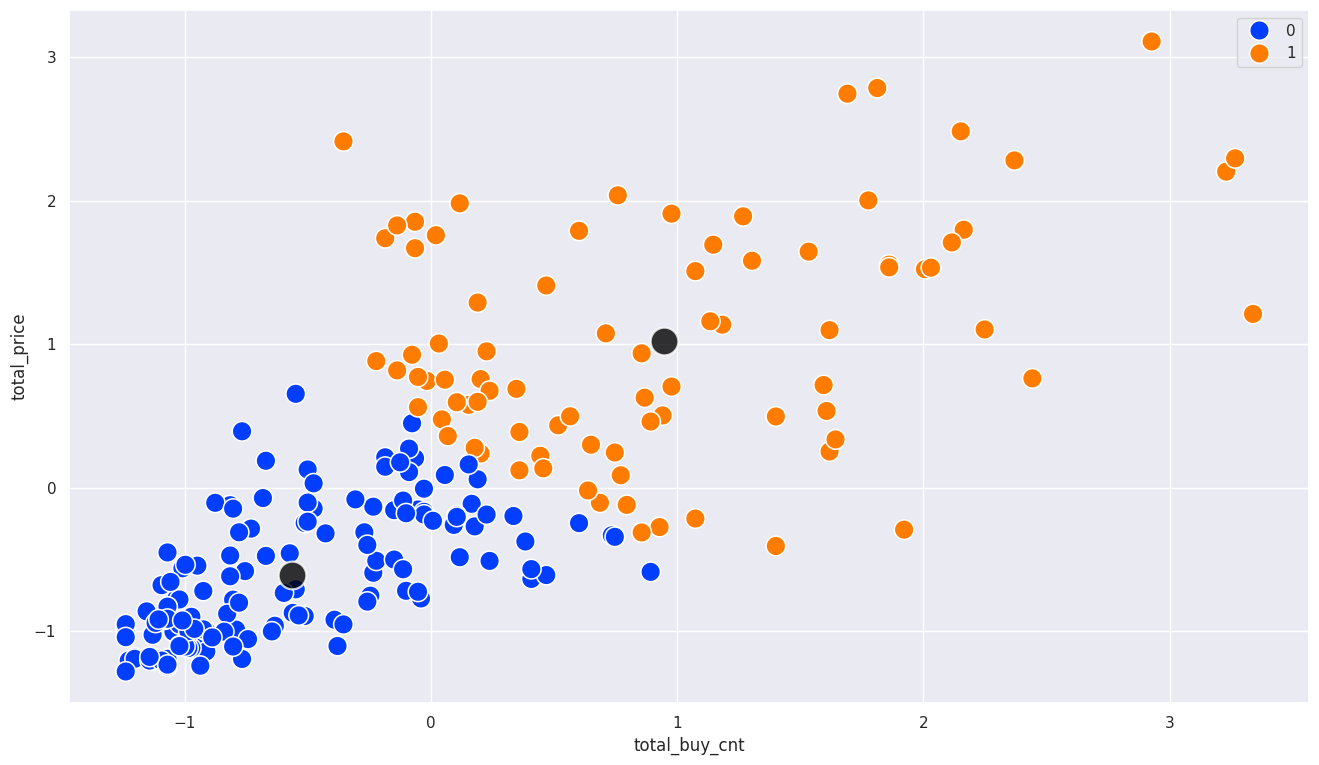
# 각 군집의 중심점
centers = model.cluster_centers_

sns.scatterplot(x=scaled_df['total_buy_cnt'], y=scaled_df['total_price'], hue=scaled_df['label'], s=200, palette='bright')
sns.scatterplot(x=centers[:,0], y=centers[:,1], color='black', alpha=0.8, s=400)

<Axes: xlabel='total_buy_cnt', ylabel='total_price'>

최적의 k 선정 기준

K-means의 성능은 클러스터 개수(k)에 따라 달라진다. 적절한 k를 선정하기 위한 방법은?
k-means는 k갱의 centroid(중심점)에 가까이 모여 있는 데이터들을 하나의 클러스터로 묶어주는 방법이다
클러스터마다 속한 데이터와 centroid 사이 거리의 합이 작아야 클러스터링이 잘됐다고 할 수 있다
inertia(이너시아)는 각 클러스터에 속한 데이터들과 centroid 사이의 거리를 제곱해서 전부 더한 값으로 거리가 최소화됐는지 확인할 수 있다

  
# k가 2일때 이너시아 값
print(model.inertia_)

187.06526917589153

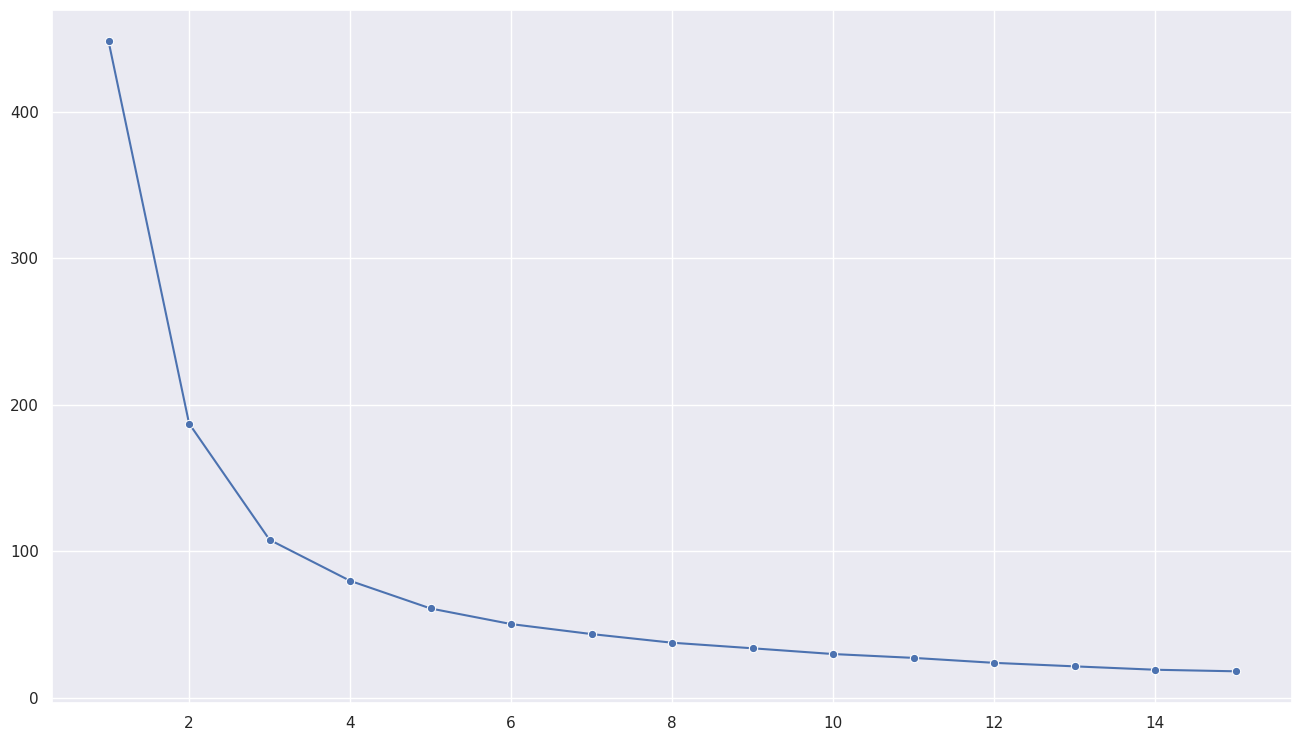
최적의 k 찾기(elbow method)
- 클러스터의 개수가 늘어날수록 이너시아값은 작아진다
- 그러나 클러스터의 개수가 많아질수록 클러스터링의 의미가 없어지기도 한다
- 따라서 적절한 클러스터의 개수는 그래프의 기울기가 급격하게 줄어드는 구간을 선택한다
- 아래 시각화에서는 k값이 2 또는 3에서 기울기가 급격하게 줄어드는 최적의 값이다
- 이처럼 그래프의 모양이 팔꿈치처럼 줄어드는 시각화로 최적의 k를 찾는 방법이 엘보우기법(elbow method) 방법이다
- 다만, 엘보우기법이 만능은 아니고, 상황이나 목적에 따라 엘보우기법과 상관없이 k의 개수를 선택하기도 한다

  
import warnings
warnings.filterwarnings(action='ignore')
# scaled_df label 열 제거
scaled_df = scaled_df.drop(['label'], axis=1)

# 1~15 k의 이너시아 값 확인
inertias = []
for k in range(1, 15 + 1):
    model = KMeans(n_clusters=k, random_state=123)
    model.fit(scaled_df)
    inertias.append(model.inertia_)

# k값에 따른 inertia값 시각화
sns.lineplot(x=range(1,15+1), y=inertias, marker='o')

<Axes: >

클러스터링 결과 해석(k-means)

  
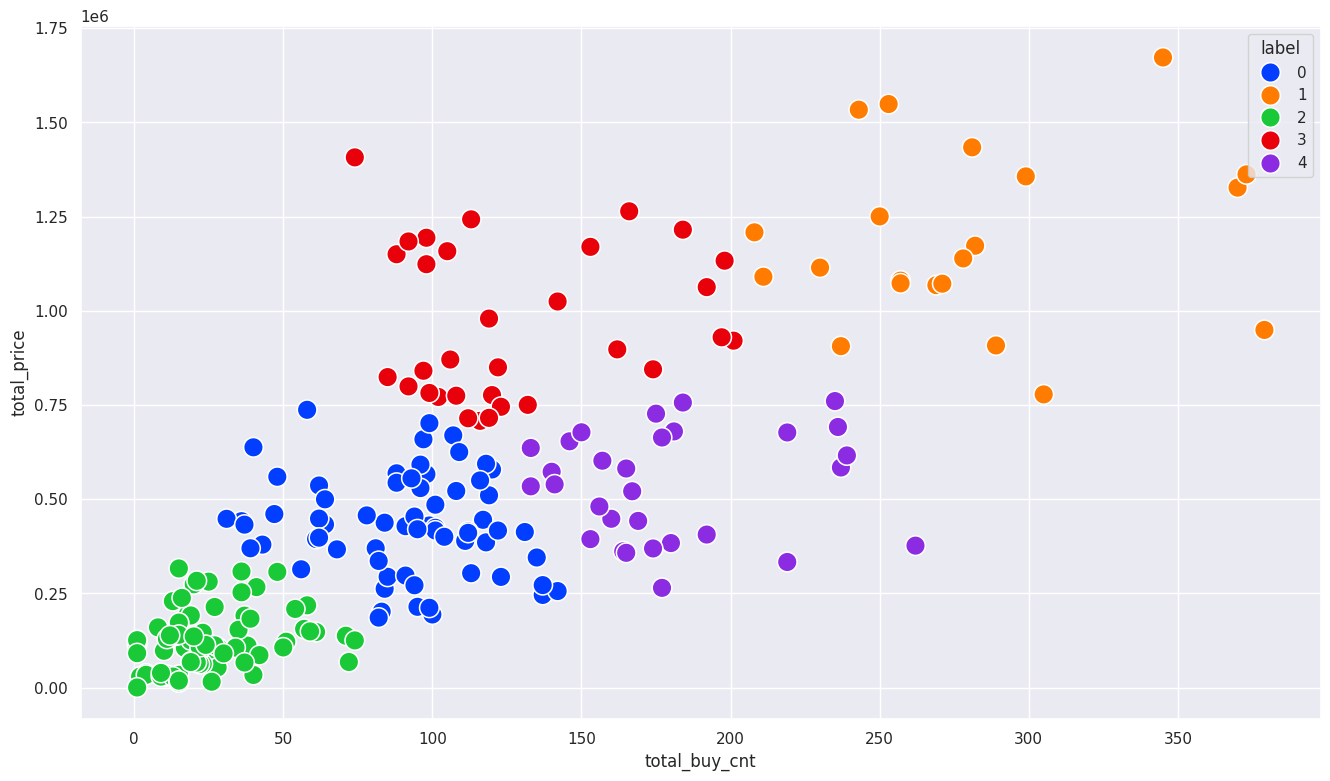
# k = 5
model = KMeans(n_clusters=5, random_state=21)
model.fit(scaled_df)

# 클러스터 구분
sales_df['label'] = model.predict(scaled_df)

# 결과 시각화
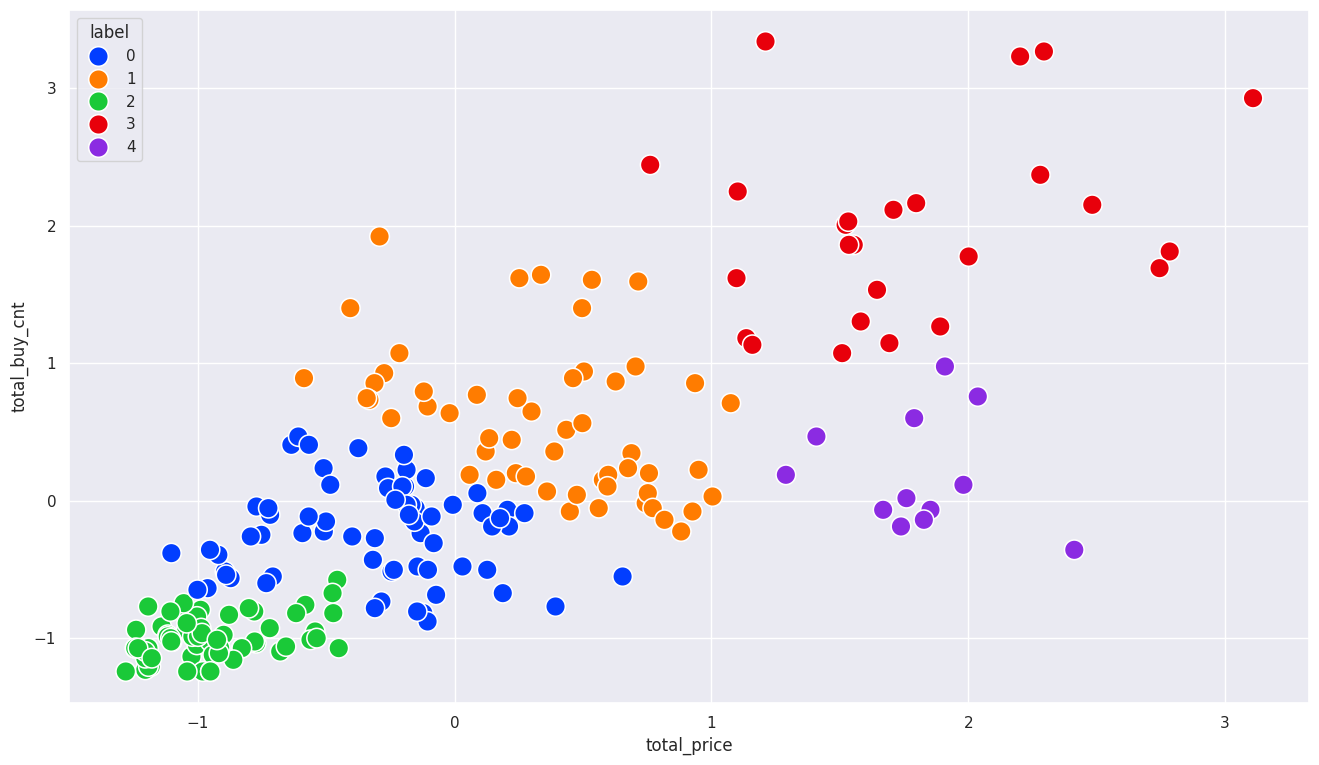
sns.scatterplot(x= sales_df['total_buy_cnt'], y=sales_df['total_price'], hue=sales_df['label'], s=200, palette='bright')

<Axes: xlabel='total_buy_cnt', ylabel='total_price'>

고객 수 확인 : 클러스터 2의 고객이 76명으로 가장 많고, 클러스터 1의 고객이 21명으로 가장 적음

  
pd.DataFrame(sales_df['label'].value_counts())

	count
label
2	76
0	66
3	32
4	30
1	21

각 클러스터별 구매 행동 특징

클러스터 0 : 총 구매수량과 금액도 일반적이고 개당 구매 가격도 보통 수준인 고객
클러스터 1 : 총 구매수량과 금액이 가장 많지만 개당 구매 가격은 적은편으로 가격이 낮은 물품들을 많이 구매하는 고객들
클러스터 2 : 총 구매수량이 적고 금액도 가장 낮은 고객으로 개당 구매 가격은 평균수준인 고객
클러스터 3 : 총 구매 수량이 많은 편은 아니지만, 구매한 품목의 평균 금액은 높은 편으로 비싼 물품을 사는 고객들
클러스터 4 : 총 구매 수량이 비교적 많지만 구매 금액이 적고 개당 구매 가격도 가장 낮은 저렴한 물품을 구매하는 고객들

  
# 각 클러스터별 구매 행동 특징
groupby_df = sales_df.groupby('label').mean()
groupby_df['price_mean'] = groupby_df['total_price'] / groupby_df['total_buy_cnt']
groupby_df

	total_buy_cnt	total_price	price_mean
label
0	90.36	430,419.85	4,763.20
1	280.33	1,192,478.57	4,253.79
2	25.46	124,004.74	4,870.47
3	127.78	963,223.12	7,538.06
4	179.53	536,416.00	2,987.84

K-means의 장단점

장점 :
- 각 변수(특성)들에 대한 배경지식, 역할, 영향도에 대해 모르더라도 데이터 사이의 거리만 구할 수 있다면 사용할 수 있다.
- 알고리즘이 비교적 간단하여 이해와 해석이 용이하다
단점 :
- 최적의 클러스터 개수인 k를 정하는게 어려울 수 있다. elbow method등의 방법으로 추론할 수 있지만 항상 정답은 아니다.
- 이상치에 영향을 많이 받는다. 이상치가 포함될 경우 중심점 위치가 크게 변동될 수 있고 클러스터가 원치않게 묶여질 수 있다.
- 차원이 높은 데이터에 적용할 때 성능이 떨어진다
단점 보완 : 중심점을 찾아주는 과정을 보안해주는 k-means++ 모델 등장

# from sklearn.cluster import KMeans
# model = KMeans(n_clusters=k, init='k-means++')

차원의 저주

차원의 저주란 변수(차원)가 많아질수록 모델의 성능이 나빠지는 현상을 말한다
1000개의 데이터를 1차원에서 2차원…3차원… 차원이 증가하면 더 많은 정보를 얻지만 데이터 간의 거리가 멀어진다
데이터 간의 거리가 멀어질수록 클러스터링 진행 시 데이터 간 유사성을 계산하는데 어렵고 정확하지 않다
특히 k-means와같이 거리 기반 모델의 성능이 현저하게 나빠질 수 있다

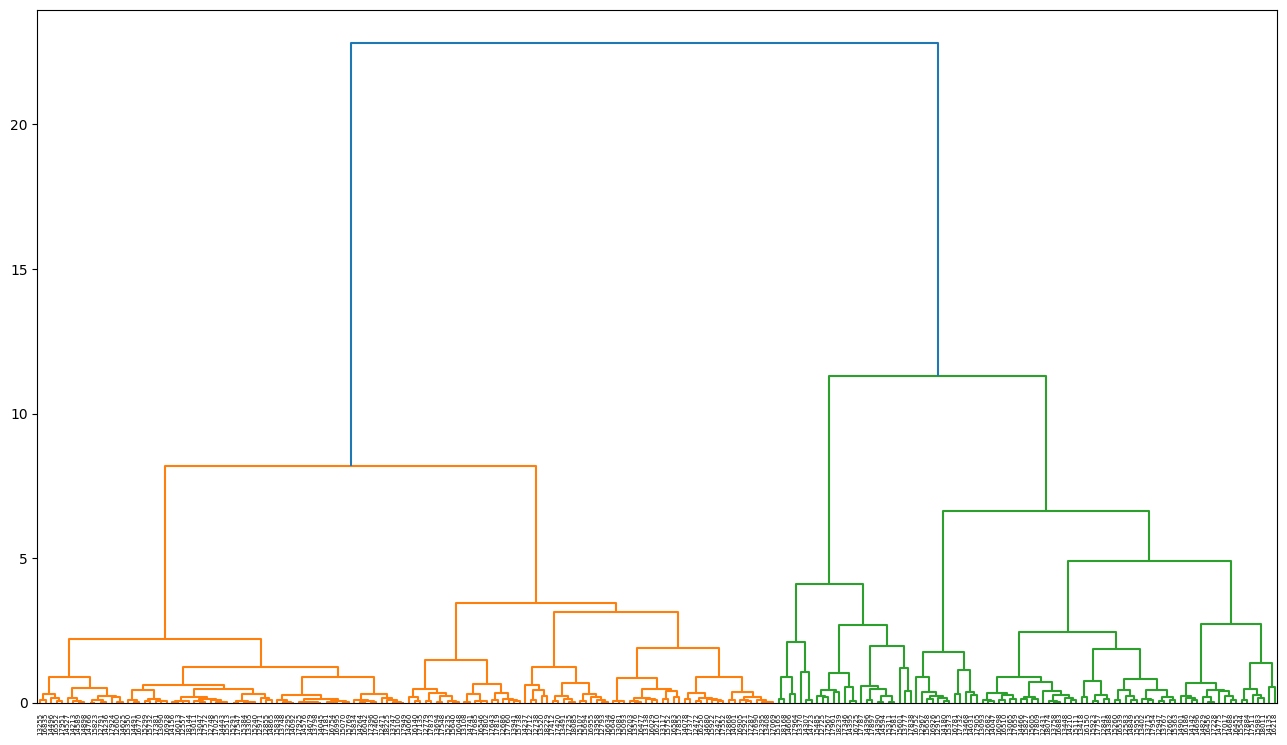
계층적 클러스터링(hierachical clustering)

순차적으로 유사한 데이터끼리 같은 클러스터로 묶어 나가는 모델로 데이터를 아래서부터 묶어 나간다고 해서 bottom-up 클러스터링이라고도 한다
각 데이터 사이의 거리를 모두 계산하여 가장 가까운 데이터 쌍을 차례대로 묶는다
묶이 데이터 쌍 끼리도 거리를 계산하여, 가까운 쌍은 하나로 묶는다
모든 데이터가 하나의 클러스터로 묶일 때까지 이 과정을 반복한다
모든 클러스터의 계층이 구분되어 연결된 상태의 그래프를 덴드로그램이라고 한다
- 계층적 클러스터링은 이 덴드로그램을 이요하여 원하는 개수로 클러스터를 나눈다

  
from scipy.cluster.hierarchy import dendrogram, linkage, cut_tree
import matplotlib.pyplot as plt

# 계층적 클러스터링 모델 학습 : linkage()함수 사용, 파마리터로 ward 거리 메소드 사용
model = linkage(scaled_df, 'ward')

# 학습 결과 시각화
labelList = scaled_df.index

# 덴드로그램 사이즈 및 스타일 조정
plt.figure(figsize=(16,9))
plt.style.use('default')

dendrogram(model, labels=labelList)
plt.show()

  
# 클러스터를 5개로 나누기
cluster_num = 5
scaled_df['label'] = cut_tree(model, cluster_num)
pd.DataFrame(scaled_df['label'].value_counts())

	count
label
0	67
2	67
1	54
3	25
4	12

  
# 시각화
sns.set(style='darkgrid',
        rc={'figure.figsize':(16,9)})
sns.scatterplot(x=scaled_df['total_price'], y=scaled_df['total_buy_cnt'], hue=scaled_df['label'], s=200, palette='bright')

<Axes: xlabel='total_price', ylabel='total_buy_cnt'>

계층적 클러스터링 장단점

장점 :
- 모델을 학습시킬 때 클러스터의 개수를 미리 가정하지 않아도 됨
- 따라서 클러스터의 개수를 몇개로 해야할 지 모를 때 유용함
단점 :
- 모든 데이터끼리의 거리를 반복해서 계산해야 하기 때문에 많은 연산이 필요함
- 따라서 대용량 데이터에 적용하는데 어려움이 있음

DBSCAN

DBSCAN(density-based spatial clustering of applications with noise)는 밀도 기반 클러스터링 방법이고 아래와같은 전제조건이 있다
- 어떤 데이터가 특정 클러스터에 속할 경우, 클러스터 내의 다른 데이터들과 가까운 위치에 있어야 한다
DBSCAN은 다른 많은 데이터와 가까운 위치를 통해 클러스터를 구분한다
위에서 말한 클러스터 구분은 얼마나 가까운 위치에 데이터가 있어야 하는지 나타내는 반경(radius)과 반경 내에 얼마나 많은 데이터가 있어야 하는지를 나타내는 최소 데이터 개수(minimum points)를 어떻게 지정하느냐에 따라 결과가 달라진다

### DBSCAN 클러스터링 진행 과정

먼저, 특정 데이터에서 지정한 반경 내에 몇 개의 데이터가 포함되는지 탐색한다
정해진 반경 내에 최소 데이터 개수가 포함되면 하나의 클러스터로 묶는다.
만들어진 클러스터의 경계에 있는 데이터들에서 그린 반경이 서로 겹치는 경우 하나로 묶어준다
조건에 만족하지 못하고 어떠한 클러스터에도 포함되지 못한 데이터는 이상치가 된다
- 이로서 dbscan 기준에 포함되지 못하는 데이터를 제외하기 때문에 이상치에 강선(robust)한 방법이다

DBSCAN 장단점

장점 : 데이터의 밀도에 따라 클러스터를 만들기 때문에 복잡하거나 기하학적인 형태를 가진 데이터 세트에 효과적이다
단점 : 고차원 데이터일수록 데이터 간 밀도를 계산하기 어려워 연산이 많아지며 학습 속도가 느려질 수 있다

  
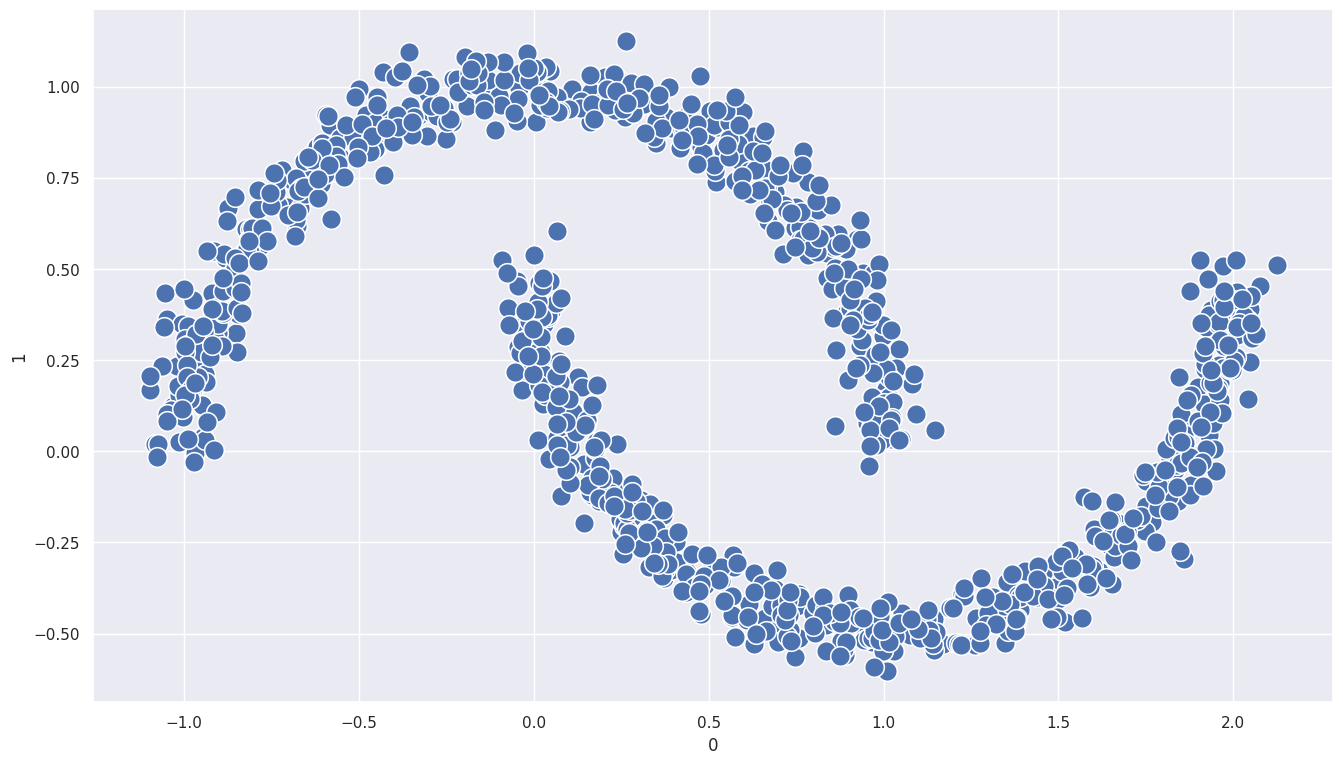
# DBSCAN 실습 데이터 생성
from sklearn.datasets import make_moons
import numpy as np

n_samples = 1000
np.random.seed(3)
x, y = make_moons(n_samples=n_samples, noise=.05)
df = pd.DataFrame(x)

# 시각화
plt.figure(figsize=(16,9))
sns.scatterplot(x=df[0], y=df[1], marker='o', s=200)

<Axes: xlabel='0', ylabel='1'>

  
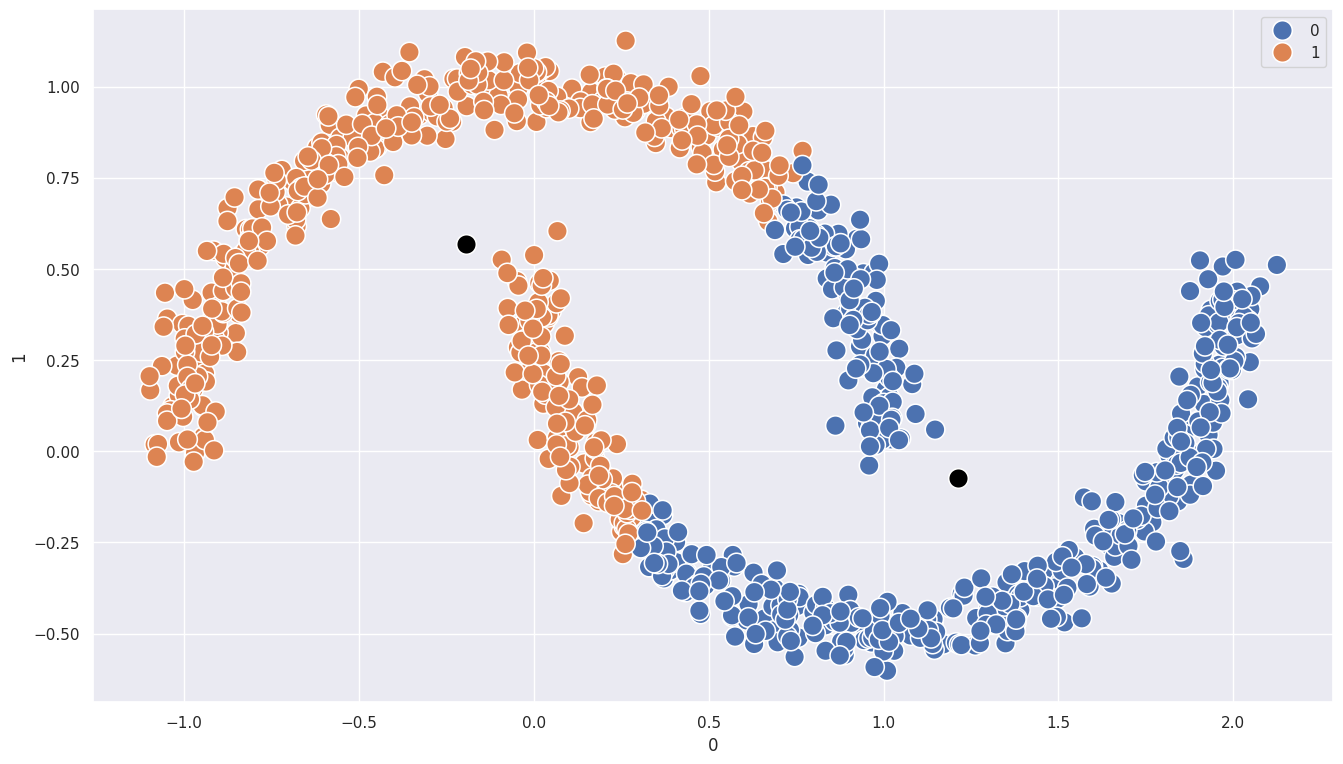
# k-means 모델 학습
model = KMeans(n_clusters=2, random_state=123)
model.fit(df)
df['kmeans_label'] = model.predict(df)
centers = model.cluster_centers_
plt.figure(figsize=(16,9))
sns.scatterplot(x=df[0], y=df[1], hue=df['kmeans_label'], s=200)
sns.scatterplot(x=centers[:,0], y=centers[:,1], color='black', s=200)

<Axes: xlabel='0', ylabel='1'>

  
# DBSCAN 모델 학습
df = df.drop(columns=['kmeans_label'], axis=1)
from sklearn.cluster import DBSCAN
eps = 0.1 # 반경
min_samples = 5 # 최소 데이터 개수

model = DBSCAN(eps=eps, min_samples=min_samples)
model.fit(df)
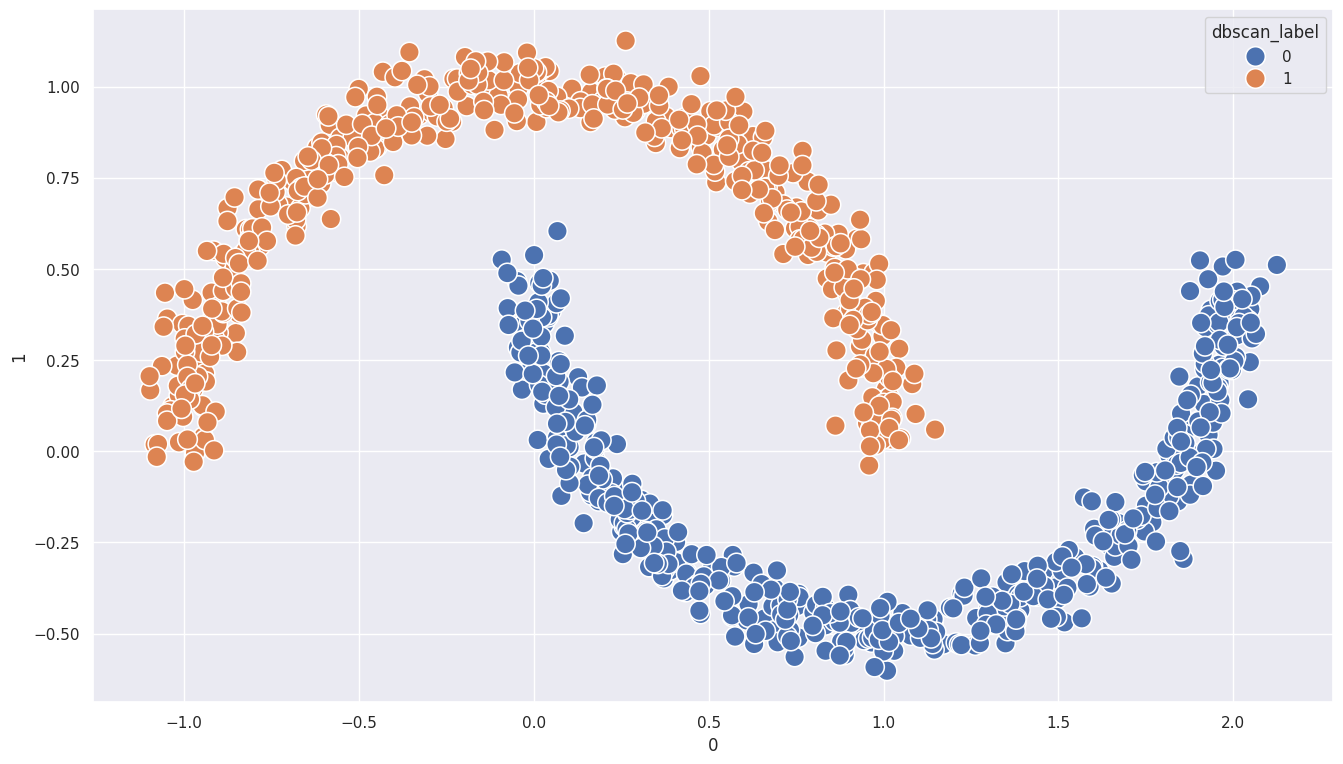
df['dbscan_label'] = model.labels_

# 시각화
plt.figure(figsize=(16,9))
sns.scatterplot(x=df[0], y=df[1], hue=df['dbscan_label'], s=200)

<Axes: xlabel='0', ylabel='1'>

GMM(gaussian mixture model)

GMM은 데이터가 서로 다른 k 개의 정규분포에서 생성되었다고 가정하는 모델 기법
- 정규분포란 평균을 중심으로 대칭이며 표준편차에 따라 흩어진 정도가 정해지는 분포
데이터가 정규 분포를 따를 때 값이 특정 구간에 속할 확률을 계산할 수 있고, GMM은 이 확률을 통해 클러스터를 구분한다
특정 데이터의 값이 어떤 분포에 포함될 확률이 더 큰지를 따져서 각 클러스터로 구분하는게 GMM 방법이다
GMM을 사용하면 데이터가 단순한 원형 분포 뿐만 아니라 타원형이나 비대칭 등의 데이터도 효과적으로 클러스터링을 할 수 있다
다만, k-means와 비슷하게 사전에 클러스터 개수를 설정해야 하며, k의 개수에 따라 결과가 달라질 수 있다
또한, 특정 분포에 할당되는 데이터 수가 적으면 모수 추정이 잘 이뤄지지 않아 많은 수의 데이터가 없으면 적용하기 어렵다
그리고 정규분포가 아닌 범주형 데이터 등에는 다룰 수 없다

  
# GMM 데이터 샘플 생성
from sklearn.datasets import make_blobs
n_samples = 500
centers = 4  # 클러스터 수
cluster_std = 0.75 # 클러스터 내 표준편차
random_state = 13

data, clusters = make_blobs(n_samples=n_samples, centers=centers, cluster_std=cluster_std, random_state=random_state)

tf = [[0.6, -0.6], [-0.4, 0.2]]
data_tf = data @ tf
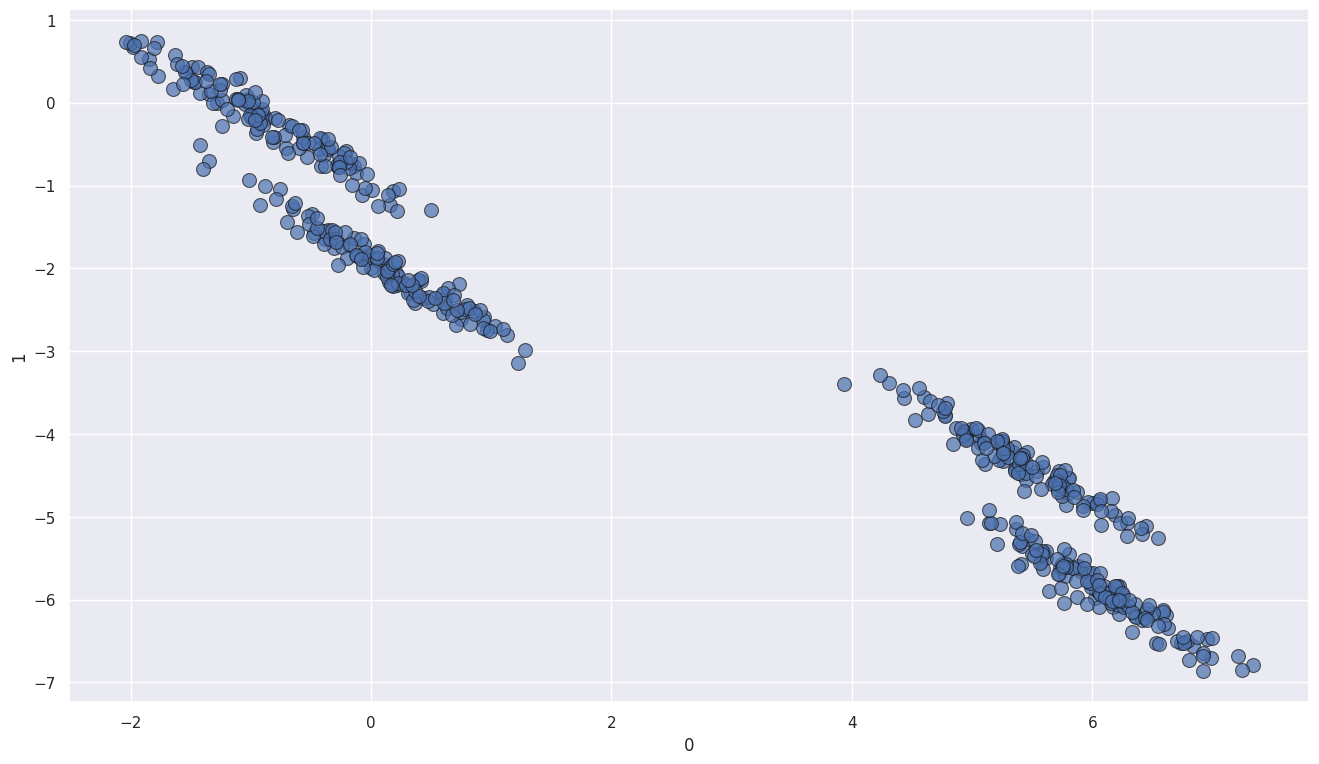
df = pd.DataFrame(data_tf)

# 시각화
sns.scatterplot(x=df[0], y=df[1], alpha = 0.7, edgecolor='k', s=100)

<Axes: xlabel='0', ylabel='1'>

  
# k-means 모델 학습
model = KMeans(n_clusters=4, random_state=123)
model.fit(df)
df['kmeans_label'] = model.predict(df)
centers = model.cluster_centers_

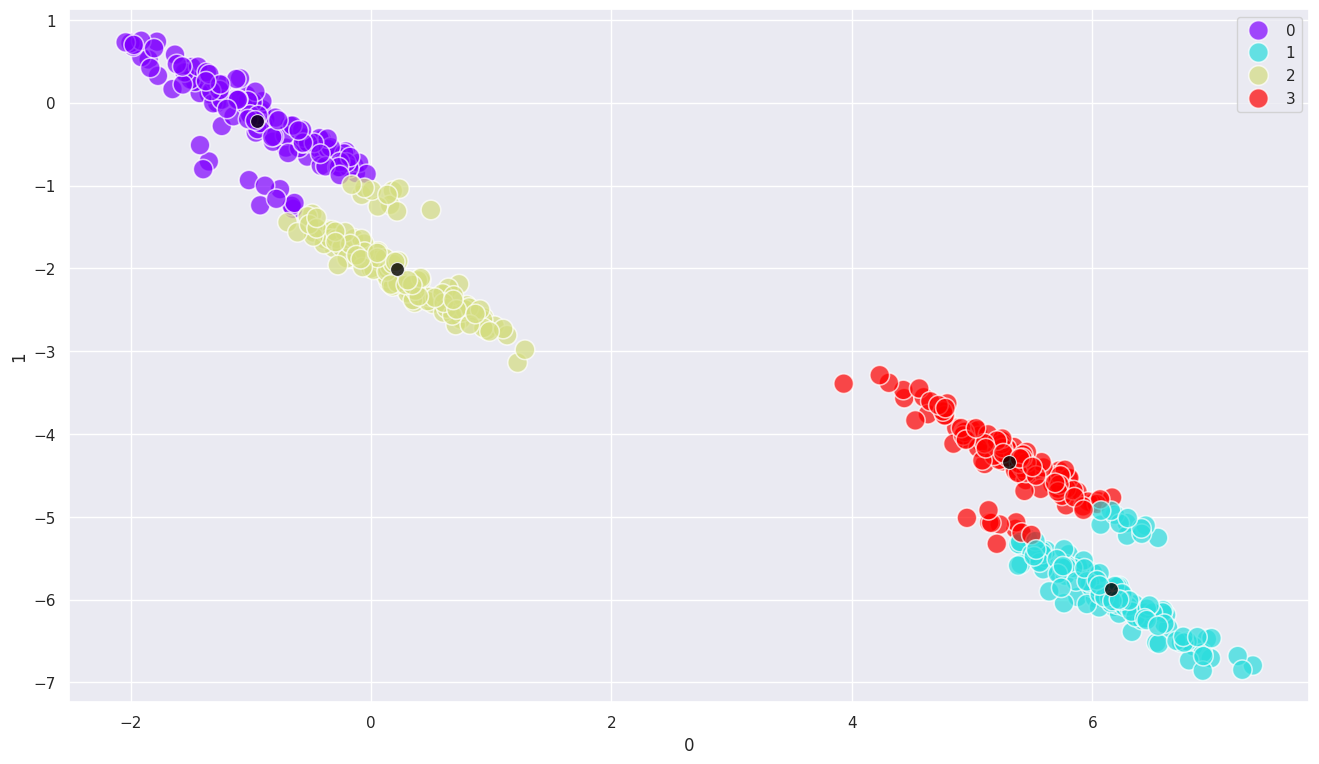
# 시각화
sns.scatterplot(x=df[0], y=df[1], hue=df['kmeans_label'], palette='rainbow', alpha=0.7, s=200)
sns.scatterplot(x=centers[:,0], y=centers[:,1], color='black', alpha=0.8, s=100)

<Axes: xlabel='0', ylabel='1'>

  
# GMM 클러스터링
df = df.drop(columns=['kmeans_label'], axis=1)

from sklearn.mixture import GaussianMixture
n_components = 4
random_state = 10
model = GaussianMixture(n_components=n_components, random_state=random_state)

# GMM 모델 학습
model.fit(df)
df['gmm_label'] = model.predict(df)

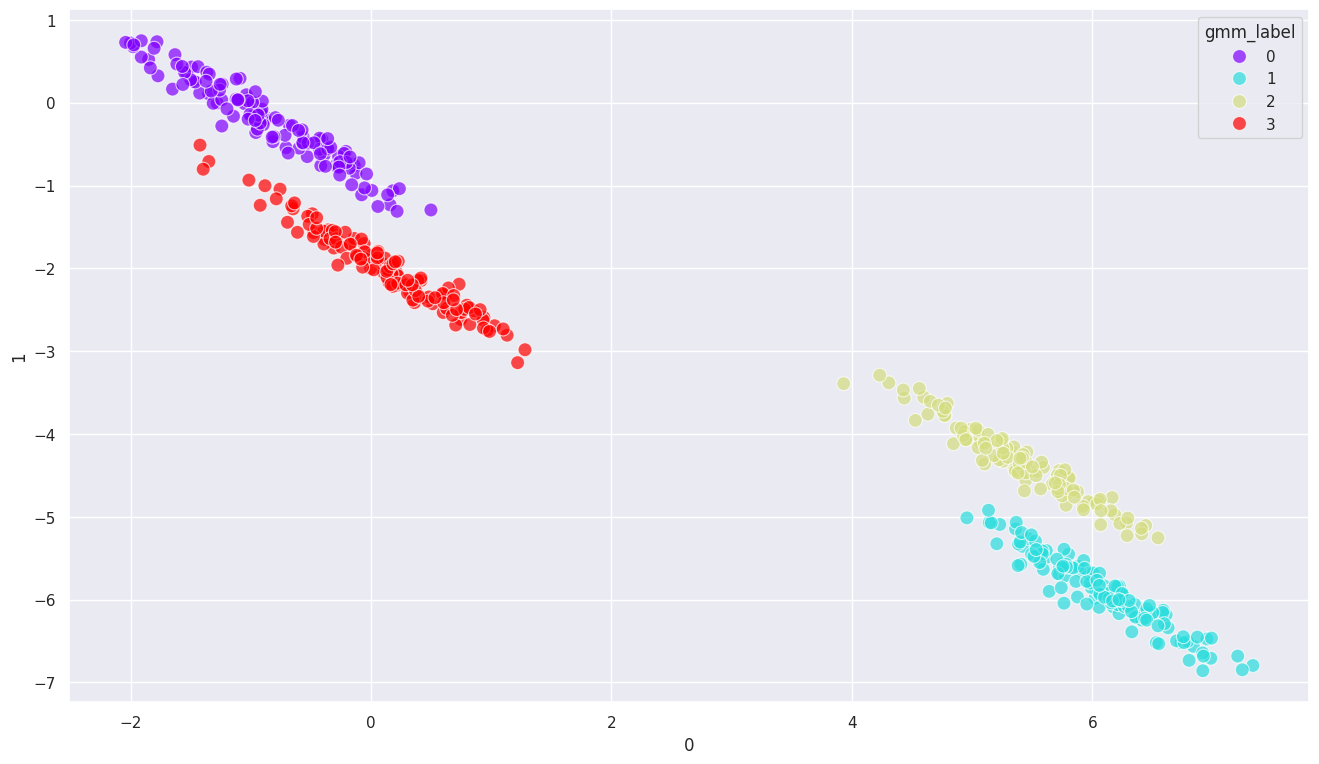
# 시각화
sns.scatterplot(x=df[0], y=df[1], hue=df['gmm_label'], palette='rainbow', alpha=0.7, s=100)

<Axes: xlabel='0', ylabel='1'>

주성분분석 PCA(principal component analysis)

주성분분석(PCA)은 대표적인 차원 축소 기법 중 하나로 여러 차원들의 특징을 가장 잘 설명해 주는 차원인 주성분(principal component)을 이용하여 차원을 축소하는 방법
주성분분석을 원활하게 하기 위해서는 변수 간 단위를 통일해 주는 과정이 필요하며, 정규화나 표준화를 사용함
주성분은 데이터들의 중심(원점)을 지나면서 모든 데이터들에서의 수직 거리의 합이 가장 가깝도록 하는 선을 말함
주성분을 찾아 데이터를 투영(projection, 데이터들을 주성분 위로 옮기는 과정)하여 모든 데이터들을 주성분 위에 위치하게 함
새롭게 만들어진 변수인 주성분(PC1, PC2…)을 축으로 만들어 시각화함

주성분을 찾는 방법

데이터들의 중심(원점)을 지나면서 모든 데이터들에서의 수직 거리의 합이 가장 가깝도록 하는 선을 찾는다
- 찾은 주성분으로 데이터들을 투영했을 때, 해당 데이터가 퍼져있는 정도(분산)가 커진다. 즉 분산이 최대가 되도록 하는 선이 데이터에 대한 설명력이 가장 높다

  
user = pd.read_csv('/content/drive/MyDrive/custom_data.csv')
user.head()

	recency	age	children	spent_all	purchase_num_all	family_size
0	58	66	0	1617	25	1
1	38	69	2	27	6	3
2	26	58	0	776	21	2
3	26	39	1	53	8	3
4	94	42	1	422	19	3

  
# 데이터 스케일링
user_mean = user.mean()
user_std = user.std()
scaled_df = (user - user_mean) / user_std

  
from sklearn.decomposition import PCA

# 모델 생성 : 2차원 축소 지정
pca = PCA(n_components=2)

# 모델 학습
pca.fit(scaled_df)

# PC로 데이터 변환
scaled_df_pca = pca.transform(scaled_df)
pca_df = pd.DataFrame(scaled_df_pca)

pca_df.columns = ['PC1', 'PC2'] # 데이터프레임 이름 지정

pca_df.head()

	PC1	PC2
0	-3.04	0.65
1	1.93	0.53
2	-1.50	-0.12
3	1.17	-1.37
4	0.23	-0.08

  
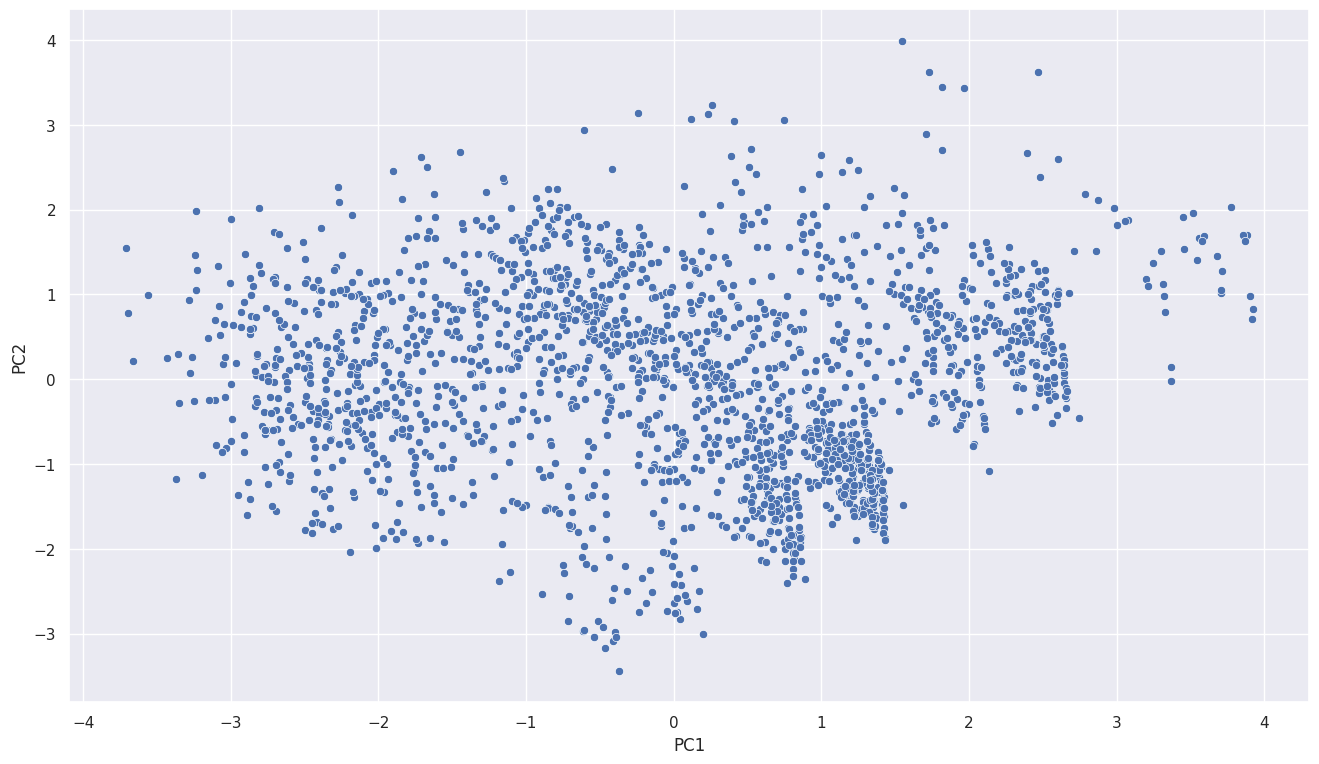
# PCA 시각화
sns.scatterplot(data=pca_df, x='PC1', y='PC2')

<Axes: xlabel='PC1', ylabel='PC2'>

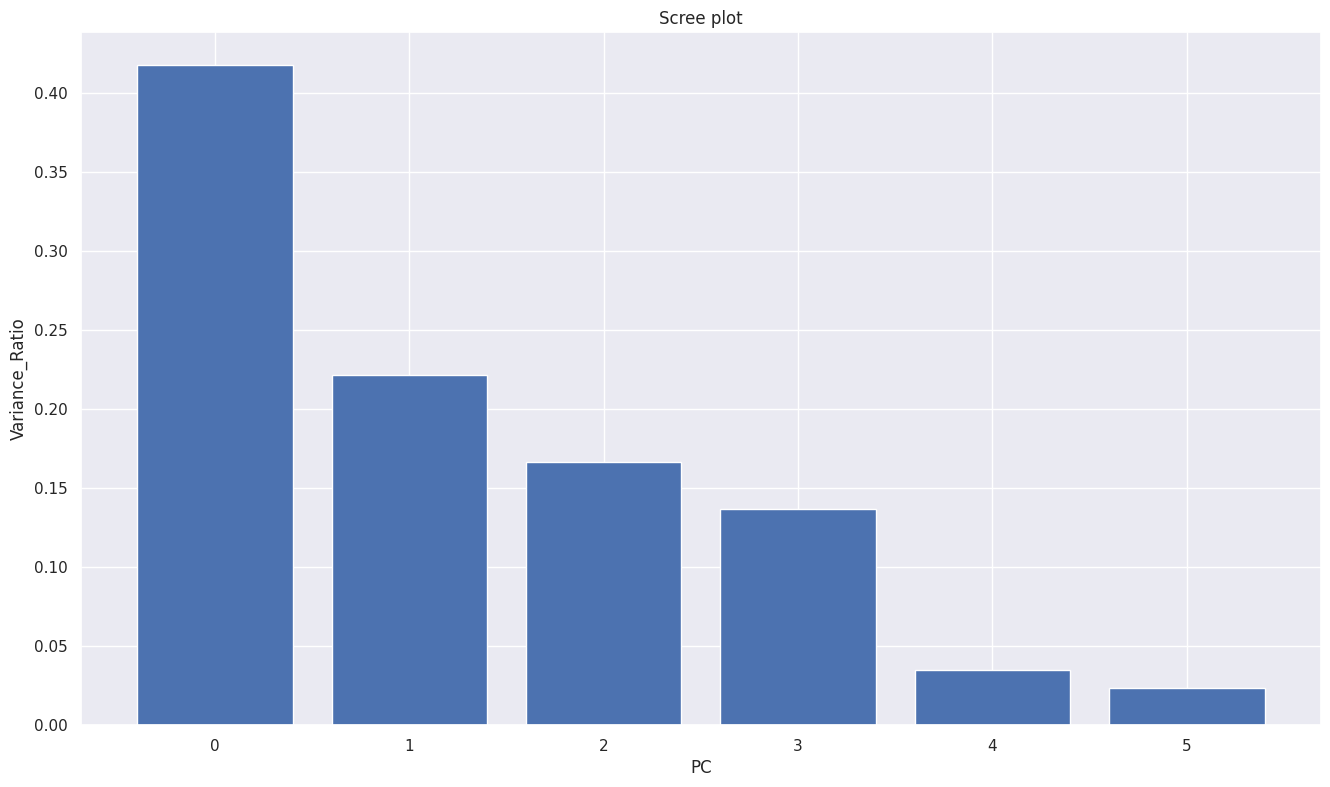
적절한 주성분 수 구하기 : scree plot

scree plot은 각 주성분이 전체 데이터에 대해서 갖는 설명력 비율을 시각화한 플롯
전체 주성분의 분산 대비 특정 주성분의 분산의 비율을 시각화 한 것
주성분 분산 비율의 합을 누적했을 때 전체 대비 70% 이상이 되는 PC_N을 고르는 방법

  
# 6차원에서 PC가 각각 전체 데이터에 대해서 어느 정도의 설명력을 가지는지,
# 전체 분산 대비 어느 정도의 분산 비율을 가지는지 확인
pca = PCA(n_components=6)
pca.fit(scaled_df)
scaled_df_pc = pca.transform(scaled_df)
pca_df = pd.DataFrame(scaled_df_pc)
pca_df.columns = ['PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6']

# PCA 개수
num_components = len(pca.explained_variance_ratio_)

x = np.arange(num_components)
var = pca.explained_variance_ratio_

plt.bar(x, var)

plt.xlabel('PC')
plt.ylabel('Variance_Ratio')
plt.title('Scree plot')

plt.show()

  
# 주성분들의 누적 분산 비율 확인
cum_var = np.cumsum(var)
cum_vars = pd.DataFrame({'cum_vars': cum_var}, index = pca_df.columns)
cum_vars
# 주성분을 3개로 차원을 축소하는게 80% 정도의 설명력을 가져 적절할 수 있다

	cum_vars
PC1	0.42
PC2	0.64
PC3	0.80
PC4	0.94
PC5	0.98
PC6	1.00

PCA 실제 예제 활용

  
credit_df1 = pd.read_csv('/content/drive/MyDrive/CC_GENERAL.csv')
credit_df1.head(10)

	CUST_ID	BALANCE	BALANCE_FREQUENCY	PURCHASES	ONEOFF_PURCHASES	INSTALLMENTS_PURCHASES	CASH_ADVANCE	PURCHASES_FREQUENCY	ONEOFF_PURCHASES_FREQUENCY	PURCHASES_INSTALLMENTS_FREQUENCY	CASH_ADVANCE_FREQUENCY	CASH_ADVANCE_TRX	PURCHASES_TRX	CREDIT_LIMIT	PAYMENTS	MINIMUM_PAYMENTS	PRC_FULL_PAYMENT	TENURE
0	C10001	40.90	0.82	95.40	0.00	95.40	0.00	0.17	0.00	0.08	0.00	0	2	1,000.00	201.80	139.51	0.00	12
1	C10002	3,202.47	0.91	0.00	0.00	0.00	6,442.95	0.00	0.00	0.00	0.25	4	0	7,000.00	4,103.03	1,072.34	0.22	12
2	C10003	2,495.15	1.00	773.17	773.17	0.00	0.00	1.00	1.00	0.00	0.00	0	12	7,500.00	622.07	627.28	0.00	12
3	C10004	1,666.67	0.64	1,499.00	1,499.00	0.00	205.79	0.08	0.08	0.00	0.08	1	1	7,500.00	0.00	864.21	0.00	12
4	C10005	817.71	1.00	16.00	16.00	0.00	0.00	0.08	0.08	0.00	0.00	0	1	1,200.00	678.33	244.79	0.00	12
5	C10006	1,809.83	1.00	1,333.28	0.00	1,333.28	0.00	0.67	0.00	0.58	0.00	0	8	1,800.00	1,400.06	2,407.25	0.00	12
6	C10007	627.26	1.00	7,091.01	6,402.63	688.38	0.00	1.00	1.00	1.00	0.00	0	64	13,500.00	6,354.31	198.07	1.00	12
7	C10008	1,823.65	1.00	436.20	0.00	436.20	0.00	1.00	0.00	1.00	0.00	0	12	2,300.00	679.07	532.03	0.00	12
8	C10009	1,014.93	1.00	861.49	661.49	200.00	0.00	0.33	0.08	0.25	0.00	0	5	7,000.00	688.28	311.96	0.00	12
9	C10010	152.23	0.55	1,281.60	1,281.60	0.00	0.00	0.17	0.17	0.00	0.00	0	3	11,000.00	1,164.77	100.30	0.00	12

  
# 기초 통계량 확인
credit_df2 = credit_df1.drop('CUST_ID', axis = 1)

credit_df2.describe()

	BALANCE	BALANCE_FREQUENCY	PURCHASES	ONEOFF_PURCHASES	INSTALLMENTS_PURCHASES	CASH_ADVANCE	PURCHASES_FREQUENCY	ONEOFF_PURCHASES_FREQUENCY	PURCHASES_INSTALLMENTS_FREQUENCY	CASH_ADVANCE_FREQUENCY	CASH_ADVANCE_TRX	PURCHASES_TRX	CREDIT_LIMIT	PAYMENTS	MINIMUM_PAYMENTS	PRC_FULL_PAYMENT	TENURE
count	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00	8,950.00
mean	1,564.47	0.88	1,003.20	592.44	411.07	978.87	0.49	0.20	0.36	0.14	3.25	14.71	4,494.45	1,733.14	864.21	0.15	11.52
std	2,081.53	0.24	2,136.63	1,659.89	904.34	2,097.16	0.40	0.30	0.40	0.20	6.82	24.86	3,638.61	2,895.06	2,330.59	0.29	1.34
min	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	50.00	0.00	0.02	0.00	6.00
25%	128.28	0.89	39.63	0.00	0.00	0.00	0.08	0.00	0.00	0.00	0.00	1.00	1,600.00	383.28	170.86	0.00	12.00
50%	873.39	1.00	361.28	38.00	89.00	0.00	0.50	0.08	0.17	0.00	0.00	7.00	3,000.00	856.90	335.63	0.00	12.00
75%	2,054.14	1.00	1,110.13	577.40	468.64	1,113.82	0.92	0.30	0.75	0.22	4.00	17.00	6,500.00	1,901.13	864.21	0.14	12.00
max	19,043.14	1.00	49,039.57	40,761.25	22,500.00	47,137.21	1.00	1.00	1.00	1.50	123.00	358.00	30,000.00	50,721.48	76,406.21	1.00	12.00

  
# 표준화 진행
scaled_credit_df2 = (credit_df2 - credit_df2.mean()) / credit_df2.std()

  
# PCA 사용 2차원으로 차원 축소
X = scaled_credit_df2.copy()

# 객체
pca = PCA(n_components=2)

# 적용
pca.fit(X)
x_pca = pca.transform(X)
pca_df = pd.DataFrame(x_pca)
pca_df.head()

	0	1
0	-1.68	-1.08
1	-1.14	2.51
2	0.97	-0.38
3	-0.87	0.04
4	-1.60	-0.69

  
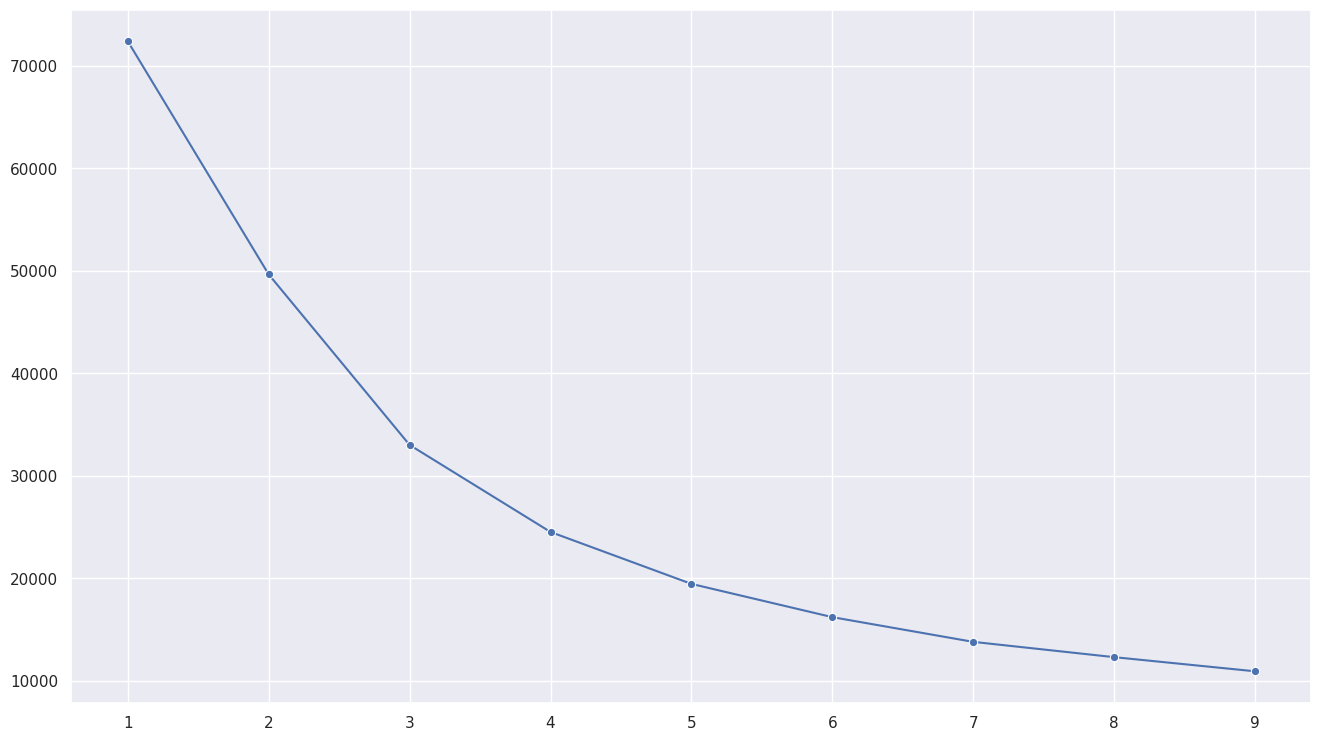
# 2차원으로 줄인 데이터를 활용하여 k-means 클러스터링 진행
ks = range(1,10)
inertias = []

for k in ks:
    model = KMeans(n_clusters=k)
    model.fit(pca_df)
    inertias.append(model.inertia_)

#시각화
sns.lineplot(x=ks, y=inertias, marker='o')

<Axes: >

  
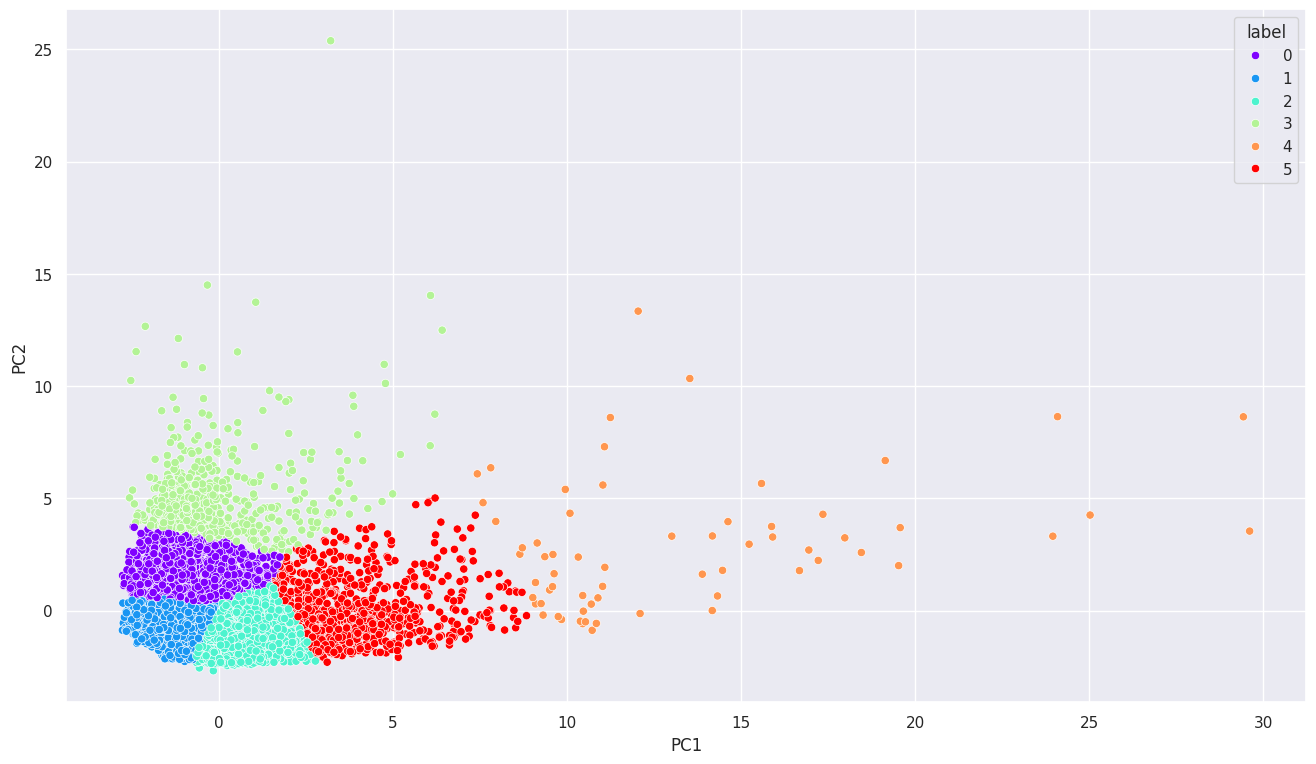
# k = 6 기준 k-means 클러스터링 진행
model = KMeans(n_clusters=6)
model.fit(pca_df)
labels = model.labels_  # 고객마다 부여할 클러스터
x, y = pca_df[0], pca_df[1]

# PCA 진행한 데이터프레임에 클러스터 번호 부여
pca_km_df = pd.DataFrame({'PC1': x, 'PC2':y, 'label':labels})

# 시각화
sns.scatterplot(data=pca_km_df, x='PC1', y='PC2', hue='label', palette='rainbow')

<Axes: xlabel='PC1', ylabel='PC2'>

  
# 클러스터 결과 해석
# k = 6인 k-means 클러스터링 진행
model = KMeans(n_clusters=6, random_state = 111)
model.fit(pca_df)

labels=model.labels_  #고객마다 부여할 클러스터

# 원본 데이터에 클러스터 부여
credit_df1['cluster'] = labels

credit_df1['CUST_ID'].groupby(credit_df1['cluster']).count()

	CUST_ID
cluster
0	2896
1	81
2	969
3	2908
4	1622
5	474

dtype: int64

  
credit_df1 = credit_df1.drop('CUST_ID', axis = 1)
credit_df1.groupby(credit_df1['cluster']).mean().T

cluster	0	1	2	3	4	5
BALANCE	645.95	5,009.79	2,306.69	722.88	2,774.36	6,093.33
BALANCE_FREQUENCY	0.90	0.98	0.98	0.76	0.95	0.98
PURCHASES	933.77	15,733.77	3,754.43	216.07	253.90	679.01
ONEOFF_PURCHASES	425.85	10,545.13	2,343.75	156.31	174.88	433.73
INSTALLMENTS_PURCHASES	508.14	5,188.65	1,411.30	60.21	79.05	245.43
CASH_ADVANCE	104.90	1,095.42	491.82	349.37	2,275.15	6,720.53
PURCHASES_FREQUENCY	0.83	0.95	0.95	0.19	0.18	0.33
ONEOFF_PURCHASES_FREQUENCY	0.24	0.79	0.65	0.07	0.09	0.17
PURCHASES_INSTALLMENTS_FREQUENCY	0.65	0.83	0.77	0.11	0.10	0.22
CASH_ADVANCE_FREQUENCY	0.02	0.09	0.07	0.08	0.34	0.58
CASH_ADVANCE_TRX	0.43	3.15	1.59	1.33	7.75	20.23
PURCHASES_TRX	17.08	140.96	53.89	2.79	3.64	9.61
CREDIT_LIMIT	3,735.86	12,996.30	7,730.80	2,809.83	5,060.09	9,459.81
PAYMENTS	1,061.80	15,869.14	3,617.19	692.45	1,896.34	5,393.90
MINIMUM_PAYMENTS	506.89	3,517.82	1,238.09	473.17	1,303.75	2,724.40
PRC_FULL_PAYMENT	0.28	0.38	0.28	0.07	0.03	0.04
TENURE	11.61	11.96	11.92	11.36	11.37	11.50

  
credit_df1.groupby(credit_df1['cluster']).mean().T.iloc[[0,1],]

cluster	0	1	2	3	4	5
BALANCE	645.95	5,009.79	2,306.69	722.88	2,774.36	6,093.33
BALANCE_FREQUENCY	0.90	0.98	0.98	0.76	0.95	0.98

클러스터 2 : 평균 잔액이 중간인 편이며 잔액 갱신 빈도가 가장 높은 고객군
클러스터 3 : 평균 잔액이 낮은 편이며 잔액 갱신 빈도가 가장 낮은 고객군
클러스터 5 : 평균 잔액이 가장 높은 편이며 잔액 갱신 빈도가 높은 편인 고객군
클러스터 4 : 평균 잔액이 중간 정도이며 잔액 갱신 빈도가 중간 정도인 고객군
클러스터 0 : 평균 잔액이 가장 낮으며 잔액 갱신 빈도가 낮은 편인 고객군
클러스터 1 : 평균 잔액이 높은 편이며 잔액 갱신 빈도가 높은 편인 고객군

Data_analysis, Python_DA_Library

Python Data_analysis

This post is licensed under CC BY 4.0 by the author.

모델과 학습

최적의 k 선정 기준

클러스터링 결과 해석(k-means)

고객 수 확인 : 클러스터 2의 고객이 76명으로 가장 많고, 클러스터 1의 고객이 21명으로 가장 적음

각 클러스터별 구매 행동 특징

K-means의 장단점

차원의 저주

계층적 클러스터링(hierachical clustering)

계층적 클러스터링 장단점

DBSCAN

DBSCAN 장단점

GMM(gaussian mixture model)

주성분분석 PCA(principal component analysis)

주성분을 찾는 방법

적절한 주성분 수 구하기 : scree plot

PCA 실제 예제 활용

Trending Tags